今天又进行了一波校内胡测
来整理一波
T1 单词序列
【问题描述】
给出两个单词(开始单词和结束单词)以及一个词典。 找出从开始单词转换到结束单词,所需要的最短转换序列。 转换的规则如下:
1、每次只能改变一个字母
2、转换过程中出现的单词(除开始单词和结束单词)必须存在于词典中
例如:
开始单词为: hit
结束单词为: cog
词典为: [hot,dot,dog,lot,log,mot]
那么一种可能的最短变换是: hit -> hot -> dot -> dog -> cog,
所以返回的结果是序列的长度 5;
注意:
1、 如果不能找到这种变换, 则输出 0;
2、 词典中所有单词长度一样;
3、 所有的单词都由小写字母构成;
4、 开始单词和结束单词可以不在词典中。
我们毫不经意的就想到了队列的做法
将起点设置为开始的单词
终点设置为目标单词
然后进行一波操作
将每一个字母进行匹配
然后能改就改(不能改就在最后cout<<0)
类似于BFS
找到最短的距离
然后输出
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<iomanip> #include<string> #include<algorithm> #include<cstdlib> #include<queue> using namespace std; struct node { string word; int ans; }s[31]; string begin,end; bool b[31],bj; int length; queue<int> q; int sum; int QwQ(string x,string y) { int sum=0; for(int i=0;i<length;i++) { if(x[i]!=y[i]) { sum++; } } return sum; } int main() { freopen("word.in","r",stdin); freopen("word.out","w",stdout); cin>>begin>>end; length=begin.size(); char ch; s[1].word=begin; int i=2; while(cin>>s[i].word) { i++; } s[i].word=end; q.push(1); while(!q.empty()) { int num=q.front(); q.pop(); if(s[num].word==end) { printf("%d",s[num].ans+1); bj=1; break; } for(int j=1;j<=i;j++) { if(QwQ(s[num].word,s[j].word)==1&&!b[j]) { s[j].ans=s[num].ans+1; q.push(j); b[j]=1; } } } if(!bj) { printf("0"); } return 0; }
T2 子集
【问题描述】
对于 n=4 时, 对应的集合 s={4,3,2,1}, 他的非空子集有 15 个依次如下:
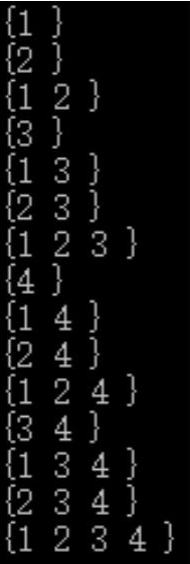
当 n=4 时, 集合{4,3,2,1}的 15 个子集分别对应于 4 位二进制数:
{1}: 0001; {2}: 0010; {1,2}: 0011; {3}: 0100, …, {1,2,3,4}: 1111。
把二进制数相对应的十进制数的 1,2,3, …,15 分别作为相应集合的编号。
如子集{1,2,4}对应的二进制数是 1011, 相应的十进制数是 11, 所以子集{1,2,4}的编号为 11。
任务:
对于给定的 n 和 m, 输出集合{1,2, …,n}的编号为 m 的子集。
【输入格式】
n,m
【输出格式】
集合的第 m 个子集的元素, 元素从小到大输出, 中间一个空格隔开。
【样例输入】
4 11
【样例输出】
1 2 4
【数据范围及约定】
100%的数据: n<=20,m<=2^n-1。
直接打暴力
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<iomanip> #include<string> #include<algorithm> #include<cstdlib> #include<queue> using namespace std; inline int read() { int X=0,w=1; char c=getchar(); while(c<'0'||c>'9') { if (c=='-') { w=-1; c=getchar(); } } while(c>='0'&&c<='9') { X=(X<<3)+(X<<1)+c-'0'; c=getchar(); } return X*w; } long long n,m; long long s[1100000]; int main() { freopen("subset.in","r",stdin); freopen("subset.out","w",stdout); n=read(); m=read(); for(int i=n-1;i>=0;i--) { if(m>=(1<<i)) { s[i]=1; m=m-(1<<i); } if(m==0) { break; } } for(int i=0;i<n;i++) { if(s[i]) { printf("%d ",i+1); } } return 0; }
T3 城市交通费
【问题描述】
有 n 个城市, 编号 1~n。 其中 i 号城市的繁华度为 pi。 省内有 m 条可以双向同行的高速
公路, 编号 1~m。 编号为 j 的高速公路连接编号为 aj 和 bj 两个城市, 经过高速公路的费用
是 wj。 若从城市 x 出发到某城市 y, 除了需要缴纳高速公路费用, 还要缴纳“城市建设费”
(为从 x 城市到 y 城市所经过的所有城市中繁华度的最大值, 包括 x 和 y 在内) 。
现提出 q 个询问, 每个询问给出一组 x 和 y, 你需要回答从 x 出发到 y 城市, 所需要的
最低交通费(高速公路费+城市建设费) 是多少。
【输入】
第一行三个整数 n,m,q。
第二行 n 个整数, 表示 p1~pn。
接下来 m 行中, 每行 3 个正整数, 第 j 行包含 Aj, Bj, Wj。
随后 Q 行每组两个正整数 x, y 表示一组询问。
【输出】
共 Q 行, 为对 Q 个问题的回答: x 城市到 y 城市的最小交通费用。
【样例输入】
5 7 2
2 5 3 3 4
1 2 3
1 3 2
2 5 3
5 3 1
5 4 1
2 4 3
3 4 4
1 4
2 3
【样例输出】
8 9
【数据范围及约定】
n≤250, m≤20000, Q≤10000, Pi≤10000, Wj≤2000, 保证任意两个城市可以互相到达。
【样例说明】
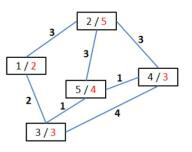
图中, 代表城市的格子中第一个数字是城市编号, 第二个红色数字是该城市的繁华度。
(1) 从城市 1 到城市 4 的最小交通费用路线是: 1 3 5 4; 公路费是 2+1+1=4; 城市建设费是
max{2,3,4,3}=4; 总交通费用 4+4=8。
(2) 从城市 2 到城市 3 的最小交通费用路线是: 2 5 3; 公路费是 3+1=4; 城市建设费是
max{5,4,3}=5; 总交通费用 4+5=9。
这个题的思路为Floyd
32行之所以排序是因为在下面的41行中要算出所经过所有点的繁华度的最大值(需要保证p【t【k】】是从第一个城市到第k个城市的最大繁华度,这样就只需要比较p【i】,p【j】和p【t【k】】就可以了)
至于40行到41行是如何实现的:
我们先假设a【i】【j】被更新,那么只有在原来未更新的f【i】【j】(=a【i】【j】+max(p【i】,p【j】))大于更新后的a【i】【j】+max(p【i】,max(p【j】,p【t【k】】))时答案f【i】【j】才会被更新
再假设a【i】【j】未被更新,那么不管p【t【k】】是大是小,答案f【i】【j】总不会受到影响
即只有a【i】【j】被更新时,才有可能更新答案
这就保证了答案的准确性
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<queue> 5 #include<algorithm> 6 using namespace std; 7 int n,m,q,p[300],aj,bj,wj,x,y,f[300][300],a[300][300],top,t[300]; 8 int cmp(int x,int y)//对繁华度的排序操作 9 { 10 return p[x]<p[y]; 11 } 12 int main() 13 { 14 freopen("road.in","r",stdin); 15 freopen("road.out","w",stdout); 16 memset(a,0x3f,sizeof(a)); 17 top=0; 18 scanf("%d%d%d",&n,&m,&q); 19 for(int i=1;i<=n;i++) 20 scanf("%d",&p[i]); 21 for(int i=1;i<=m;i++) 22 { 23 scanf("%d%d%d",&aj,&bj,&wj); 24 a[aj][bj]=min(a[aj][bj],wj);//两个城市之间会有不止一条公路 25 a[bj][aj]=min(a[bj][aj],wj);//两个城市之间会有不止一条公路 26 } 27 for(int i=1;i<=n;i++) 28 { 29 a[i][i]=0;//初始化,自己到自己为0 30 t[i]=i;//记录标号 31 } 32 sort(t+1,t+1+n,cmp);//类似于结构体,对于t数组关于p(繁华度)进行排序 33 for(int i=1;i<=n;i++) 34 for(int j=1;j<=n;j++) 35 f[i][j]=a[i][j]+max(p[i],p[j]);//算出两条直接连边公路的总价值 36 for(int k=1;k<=n;k++)//Floyd的过程 (多源最短路) 37 for(int i=1;i<=n;i++) 38 for(int j=1;j<=n;j++) 39 { 40 a[i][j]=min(a[i][j],a[i][t[k]]+a[t[k]][j]);//先算公路的代价 41 f[i][j]=min(f[i][j],a[i][j]+max(p[i],max(p[j],p[t[k]])));//算出答案 42 } 43 for(int i=1;i<=q;i++) 44 { 45 scanf("%d%d",&x,&y); 46 printf("%d ",f[x][y]);//输出 47 } 48 return 0; 49 }