优化器--牛顿法总结

---这里记录下一些关于牛顿法来作为优化器的个人笔记 ：）

关于牛顿法，先不说其中的概念，来简单看一个例子？ 不用计算器，如何手动开一个值的平方根，比如计算{sqrt(a) | a=4 } ？ 不用程序和代码如何求？

　　----比较简单有木有，直接上用公式来套就好了.

　　　　　　x_t = ( x_t-1 + ( a / x_t-1 ) ) / 2

　　　　　　我们看 sqrt(4) 这个值的区间在1<=sqrt(4)<=4里，写成这种形式吧[1,4],我们令x₀ = 1,

　　　　　　x = ( 1 + (4/1))/2 = 5/2 =2.5

　　　　　　x = (2.5 + (4/2.5))/2 = 2.05

　　　　　　x = (2.05 + ( 4 /2.05 ))/2 = 2.0006 

　　　　　　　　.....

    于是我们就求出x的近似值为2

那么这个公式是如何得来的呢？

　　这个公式其实是依据牛顿法得来的？牛顿法长成什么样子呢？

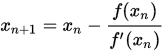　　　　 就是长成这个样子，我们发现这个样子和我们的SGD还是很像的，这两者的区别记录在后面吧～。

而牛顿迭代法，这个公式其实就是泰勒级数展开的前几项 f(x)，并使得f(x) =0，求解后的结果，而泰勒级数是采用无限项的来等价表示一个函数，比如：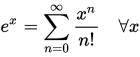

，那牛顿法采用的是泰勒级数的前几项 -- 有限的项，来近似表示一个函数f(x).

那么如何上面这个公式是如何通过牛顿法得到的呢？

　　上面的题，我们将其转换车更加通用的一些，比如改为如何求解sqrt(a)? 

 ------这又等价于sqrt(a)=x  转换成-->  x^2 = a , (a 属于实数域)，  进一步转换成--->f(x) = x^2 -a =0

我们知道 f(x) = x^2 - a =0 ，因为只要求某一个点的值，所以我们只需要知道这个点的切线就可以了， 由此我们依据泰勒级数定义，对其进行一阶展开，可以知道 f(x) ～g(x) =  f(x0) + f ' (x0)*(x - x0),我们令g(x)=0

于是我们就得到了 x = x0 - f(x0) / f '(x0);

　　然后我们再次化解这个公式：

　　　　　　　　x = x0 - (x0^2 - a / 2x0 )  = (x0^2 + a) /2x0  = (x0 + a/x0)/2

      这样我们就得到了最开始的那个公式了。

但是我们在用牛顿法作为优化器的时候，是要求极小值的啊？ 那么如何快速的求出极小值呢？

　　　我们知道一阶导，为曲线切线方向，二阶导为切线的切线方向回想一下SGD法，SGD只是在一阶导上，进行权值更新，基本上就是处于求切线方向，前进一个步长，然后再矫正，再求当前点的切线，再矫正：

　　

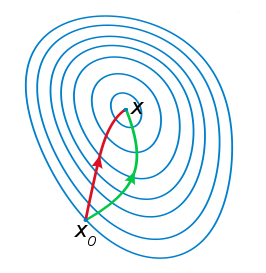
这种方式就会出现绿线的情况，那么牛顿法就給出另一种思路： 我们再沿着切线方向走的时候，不必按照固定的步长走动，我们可以依据切线的变化率来动态调整行走的步子，于是就有了这个公式：

 当二阶导趋近于0的时候，说明一阶导有极小值，那么此时就应该让它接近这个极小值，而loss函数为凸函数 ，f’(x)趋近极小值的时候，f(x)就也就可以快速的接近极小值，而不出现大幅度摇摆，就出现了红色那条线.

一般来说，对于那种高阶多项式采用牛顿法效果会比SGD好些.