Given a matrix and a target, return the number of non-empty submatrices that sum to target.
A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.
Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.
Example 1:
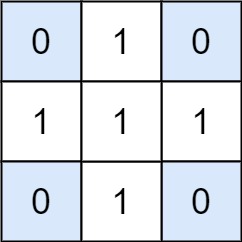
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.
Example 2:
Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
Example 3:
Input: matrix = [[904]], target = 0
Output: 0
Constraints:
1 <= matrix.length <= 1001 <= matrix[0].length <= 100-1000 <= matrix[i] <= 1000-10^8 <= target <= 10^8
这道题给了一个二维矩阵 matrix 和一个整型数 target,问有多少个非空的子矩阵使得其和正好等于 target。首先来想,这道题身为 Hard 难度,肯定不能用暴力搜索,博主之前也屡次强调过,这是一种不尊重,会惨遭 OJ 的毒打。既然是要求子矩阵之和的问题,就来想想有没有什么方法可以快速求得子矩阵之和,博主马上就联想到了之前在求子数组之和时,可以通过建立累加和数组来快速的求出任意的子数组之和。这里也可以利用相同的思路,只不过是建立的是累加和矩阵,从一维升级到了二维而已,为的就是以空间来换取时间。建立的方法比一维的稍稍复杂一些,大小为 (m+1)x(n+1),多出一位可以避免越界,然后从1开始遍历,当前位置的累加和等于上面的值加上左边的值减去左上方的值,最后加上原数组中当前位置的值,这样整个累加和矩阵就建立好了。接下来就要遍历所有子矩阵了,由于矩阵有四个端点,所以遍历是四次方的时间复杂度,不过好在有累加和矩阵,只要四个端点坐标确定了,可以在常数级的时间复杂度内求出子矩阵之和,若这个值等于 target,则结果 res 自增1即可。这个方法基本上是压线过的 OJ,多亏 OJ 仁慈,放了一马,参见代码如下:
解法一:
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int res = 0, m = matrix.size(), n = matrix[0].size();
vector<vector<int>> sums(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
sums[i][j] = sums[i][j - 1] + sums[i - 1][j] - sums[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
for (int p = 1; p <= i; ++p) {
for (int q = 1; q <= j; ++q) {
int t = sums[i][j] - sums[i][q - 1] - sums[p - 1][j] + sums[p - 1][q - 1];
if (t == target) ++res;
}
}
}
}
return res;
}
};
上面方法其实没有太多的技巧,硬说是 Hard 的难度有些牵强,再来看一种论坛上的高分解法,一种真正符合其身价的解法。这种解法的思路在之前的 Subarray Sum Equals K 和 Max Sum of Rectangle No Larger Than K 其实都出现过,有点 Two Sum 的影子在里面。话说 Two Sum 可是博主刷的第一道题呢,那个一个阳光明媚的下午,博主安静地坐在图书馆中,打开了心爱的小 Mac,登进了朋友推荐的 LeetCode 网站,从此便和力扣结下了不解之缘。如今已经刷了上千道题了,成了大家眼中的千条哥了。好了,打住打住,回到题目,具体的思路是,先建立每一行的累加和数组,这里其实将矩阵微积分化了,看作是多行的累加,有了行的累加和数组,就可以快速知道每一行的子数组之和了。接下来只要确定行的宽度就行了,即遍历任意两个列,它们之间的距离就是子矩阵的宽,然后新建一个 HashMap,建立子矩阵之和跟其出现次数之间的映射,初识时将 0->1 这个映射对儿加入,后面会讲原因。然后新建一个变量 cur,接下来遍历所有行,由于子矩阵的宽已经确定了,遍历不同行,就是进一步确定子矩阵的高,这样就能准确的确定一个子矩阵的范围了。先利用行的累加和数组来快速求出该行的数字之和,注意为了避免数组越界,需要判断一下i是否大于0。当前的子矩阵之和求出来后,保存在了 cur 之中,现在要看其和 target 之间的关系,cur 如果小于 target,则无事发生;若大于 target,则看 cur - target 是否存在,若存在,则表示和为 target 的子矩阵也必然存在,且个数跟和为 cur-target 的子矩阵相同,所以结果 res 可以直接加上 cur-target 的映射值。但是还有一种情况,当 cur 正好等于 target 的时候,cur-target 就为0了,这时候 HashMap 中0的映射值若为0,则就没法加上这种情况了,这就是为啥要将 0->1 这个映射对儿提前加入的原因。最后别忘了将 cur 的映射值自增1,参见代码如下:
解法二:
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int res = 0, m = matrix.size(), n = matrix[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 1; j < n; ++j) {
matrix[i][j] += matrix[i][j - 1];
}
}
for (int i = 0; i < n; ++i) {
for (int j = i; j < n; ++j) {
unordered_map<int, int> cntMap{{0, 1}};
int cur = 0;
for (int k = 0; k < m; ++k) {
cur += matrix[k][j] - (i > 0 ? matrix[k][i - 1] : 0);
res += cntMap[cur - target];
++cntMap[cur];
}
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1074
类似题目:
Max Sum of Rectangle No Larger Than K
参考资料:
https://leetcode.com/problems/number-of-submatrices-that-sum-to-target/