第三章作业
作业:曾是少年
二 群的性质
课上我们讲解了什么是群。请根据群定义,求解以下问题:
1. ({Z, +}) 是否为群?若是,验证其满足群定义;若不是,说明理由。
答:{Z,+}是群;
对于({Z,+}),设 (a_1in Z) , (a_2 in Z) , (a_e in Z)。
- 对于(forall a_1in Z) , (a_2 in Z), 有(a_1+a_2in Z), 因此满足封闭性。
- 对于(forall a_1in Z,a_2in Z,a_3in Z), ((a_1+a_2)+a_3 = a_1+(a_2+a_3)),因此满足结合律。
- Z中存在(0in Z),对于(forall a in Z),有(a+0=a),因此慢足幺元
- 对于(forall a in Z), 存在 (-ain Z),使得 (a+(-a) = 0),因此满足逆。
({Z,+})满足以上四条性质,因此是群
2. ({N, +}) 是否为群?若是,验证其满足群定义;若不是,说明理由。
其中(Z)为整数集,(N)为自然数集
答: ({N,+}) 不是群;
对于(forall ain N),且(a eq0),(-a otin N),不满足逆的性质要求。因此不是群。
三 验证向量叉乘的李代数性质
我们说向量和叉乘运算构成了李代数,现在请你验证它。书中对李代数的定义为:李代数由⼀个集合,V,⼀个数域 F 和⼀个⼆元运算 [, ] 组成。如果它们满足以下集几条性质,称$ (V, F, [, ])$ 为⼀个李代数,记作(g)。
-
封闭性 (∀X, Y ∈ V, [X, Y ] ∈ V).
-
双线性 (∀X, Y , Z ∈ V, a, b ∈ F), 有:
[[aX + bY , Z] = a[X, Z] + b[Y , Z], [Z, aX + bY ] = a[Z, X] + b[Z, Y ]. ] -
自反性 (∀X ∈ V, [X, X] = 0).
-
雅可比等价 (∀X, Y , Z ∈ V, [X, [Y , Z]] + [Y , [Z, X]] + [Z, [X, Y ]] = 0).
其中二元运算被称为李括号。
现取集合(V=R^3),数域(F=R),李括号为:
请验证(g=(R^3,R, imes))构成李代数。
验证:
- 封闭性
对于(forall X,Y in R^3),(X imes Y)依然是一个向量,即(X imes Y in R^3),因此满足封闭性条件。
- 双线性
对于(forall X,Y,Z in R^3),(a,bin R),向量叉乘运算满足分配律和线性性,因此有:
((aX+bY) imes Z = aX imes Z+bY imes Z = a(X imes Z)+b(Y imes Z))
(Z imes(aX+bY) = aZ imes X+bZ imes Y=a(Z imes X)+b(Z imes Y))
因此满足双线性
- 自反性
对于 (forall X in R^3),(|X imes X| = |X||X|sin0=0),因此(X imes X = 0),满足自反性。
- 雅可比等价
把三适量叉乘展开成点乘,向量的叉乘运算满足一下性质:
对于(forall X,Y,Z in R^3),
- ((X×Y)×Z=(XZ)Y-(YZ)X)
- (X imes(Y imes Z) = (XZ)Y-(XY)Z)
因此
因此向量的叉乘运算满足雅可比恒等式。
综上所述,(g=(R^3,R, imes))构成李代数
四 推导 SE(3) 的指数映射
课上给出了 SO(3) 的指数映射推导,但对于 SE(3),仅介绍了结论,没有给出详细推导。请你完成SE(3) 指数映射部分,有关左雅可比的详细推导。
设(xi = [ ho,phi]^Tin se(3)),它的指数映射为:
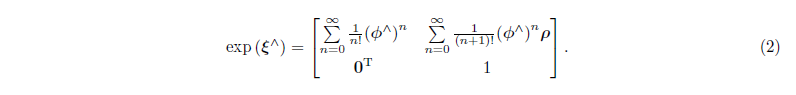
令(phi = heta a),那么:
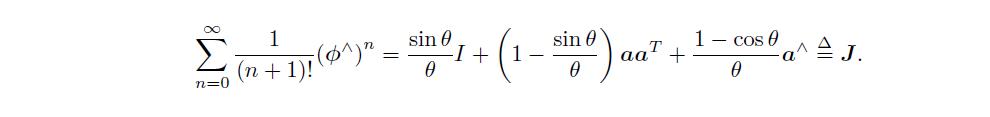
这也正是课件里提到的左雅可比。
答:令(phi = heta a)
其中:
所以:
即:
五 伴随
在SO(3) 和SE(3) 上,有⼀个东西称为伴随(Adjoint)。下面请你证明SO(3) 伴随的性质。
对于SO(3),有:
此时称Ad(R) = R。
提示:首先你需要证明(forall ain R^3,Ra^{wedge}{R^T} = (Ra)^{wedge}),[页面](https://math.stackexchange.com/questions/
2190603/derivation-of-adjoint-for-so3) 提示了⼀种简洁的途径。
对于SE(3),有:
其中Ad(T)定义为:
这个性质将在后文的Pose Graph 优化中用到。但是SE(3) 的证明较为复杂,不作要求。
完整的SO(3) 和SE(3) 性质见1和2。
证明:
我们先来证明(Ra^{wedge}R^T=(Ra)^{wedge}),过程如下:·
我们可以通过使等式的RHS作用于任意向量v来证明该等式:
因此得到:
而R是正交矩阵,因此
令( ho= heta a)
证毕。
拓展:伴随表示
在数学中,一个李群 G 的伴随表示(adjoint representation)或伴随作用(adjoint action)是 G 在它自身的李代数上的自然表示。这个表示是群 G 在自身上的共轭作用的线性化形式。

六 轨迹的描绘
我们通常会记录机器人的运动轨迹,来观察它的运动是否符合预期。大部分数据集都会提供标准轨迹以供参考,如 kitti、TUM-RGBD 等。这些文件会有各自的格式,但首先你要理解它的内容。记世界坐标系为 W,机器⼈坐标系为 C,那么机器人的运动可以用 (T_{WC}) 或 (T_{CW}) 来描述。现在,我们希望画出机器⼈在世界当中的运动轨迹,请回答以下问题:
-
事实上,(T_{WC}) 的平移部分即构成了机器人的轨迹。它的物理意义是什么?为何画出 (T_{WC}) 的平移部分就得到了机器⼈的轨迹?
答:物理意义: (T_{WC})指的是从世界坐标系原点到相机中心的平移向量;
世界坐标系不随相机运动变化,因此可以认为(T_{wc})是机器人相对于原点坐标在移动, 移动可视化在观察者眼中就是是机器人的运动轨迹
-
我为你准备了⼀个轨迹文件(code/trajectory.txt)。该文件的每⼀行由若干个数据组成,格式为
[[t, t_x, t_y, t_z, q_x, q_y, q_z, q_w] ]其中 t 为时间,(tx, ty, tz) 为 (T_{WC}) 的平移部分,(q_x, q_y, q_z, q_w) 是四元数表示的 (T_{WC}) 的旋转部分,(q_w)为四元数实部。同时,我为你提供了画图程序
draw_trajectory.cpp文件。该⽂件提供了画图部分的代码,请你完成数据读取部分的代码,然后书写CMakeLists.txt以让此程序运行起来。注意我们需要用到Pangolin库来画图,所以你需要事先安装Pangolin(如果你做了第⼀次作业,那么现在已经安装了)。CMakeLists.txt可以参照ORB-SLAM2部分。答:实现过程:使用fstream读取文件中的数据,在编译的时候遇到一点小bug,不过都解决了.
读取数据的代码块如下:
double t,t_x,t_y,t_z,q_x,q_y,q_z,q_w; while(!inFILE.eof()) { inFILE>>t; inFILE>>t_x; inFILE>>t_y; inFILE>>t_z; inFILE>>q_x; inFILE>>q_y; inFILE>>q_z; inFILE>>q_w; poses.push_back(Sophus::SE3(Eigen::Quaterniond(q_w,q_x,q_y,q_z),Eigen::Vector3d(t_x,t_y,t_z))); }运行结果如下所示;
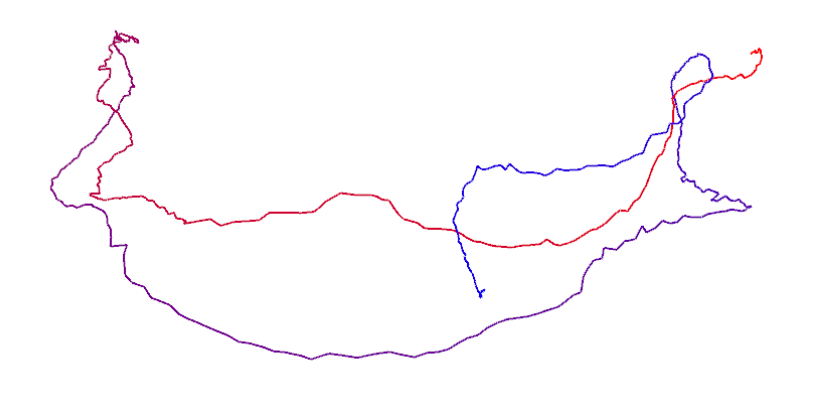
该图中:轨迹首尾颜色不一样,通过观察,发现是着色函数设置的颜色随位置变化.
附加题 七 轨迹的误差
除了画出真实轨迹以外,我们经常需要把 SLAM 估计的轨迹与真实轨迹相比较。下面说明比较的原理,请你完成比较部分的代码实现。
设真实轨迹(ground-truth)为 (T_g),估计轨迹 (T_e)。它们都以 (T_{WC}) 的形式存储,格式同上题。现在,你需要计算估计轨迹的误差。我们假设每⼀个 (T_g) 都与给定的 (T_e) 对应。那么,对于任意第 i 个位姿,它的误差可定义为:
即两个位姿之差的李代数二范数。于是,可以定义两条轨迹的均方根(Root-Mean-Square-Error, RMSE)误差为:
我为你准备了 code/ground-truth.txt 和 code/estimate.txt 两条轨迹。请你根据上⾯公式,实现 RMSE的计算代码,给出最后的 RMSE 结果。作为验算,参考答案为:2.207。
注:
-
实际当中的轨迹比较还要更复杂⼀些。通常
ground-truth由其他传感器记录(如 vicon),它的采样频率通常高于相机的频率,所以在处理之前还需要按照时间戳对齐。另外,由于传感器坐标系不一致致,还需要计算两个坐标系之间的差异。这件事也可以⽤ ICP 解得,我们将在后面的课程中讲到。 -
你可以用上题的画图程序将两条轨迹画在同⼀个图里,看看它们相差多少。
答:添加的代码主要包括三部分:
-
读取两个文件
ground-truth.txt和estimate.txt,该部分与上一题中的相同。 -
计算rmse,对于已经得到的两个pose集合,可以通过以下代码计算。
double calculateRMSE(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> truth_poses,vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> estimated_poses) { double rmse=0.0; for(int i = 0;i<truth_poses.size();i++) { Eigen::Matrix<double ,6,1> se3; se3 = (truth_poses[i].inverse()*estimated_poses[i]).log(); //这里是通过一个把其中一个变换乘以一个逆变换得到一个差矩阵,再通过.log()可以转换为向量形式 rmse+=se3.squaredNorm(); } rmse = sqrt(rmse/(double)truth_poses.size()); return rmse; } -
画图,修改轨迹绘制代码,函数部分代码如下所示:
while (pangolin::ShouldQuit() == false) { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); d_cam.Activate(s_cam); glClearColor(1.0f, 1.0f, 1.0f, 1.0f); glLineWidth(2); for (size_t i = 0; i < truth_poses.size() - 1; i++) { glColor3f(1.0f, 0.0f, 0.0f); glBegin(GL_LINES); auto p1 = truth_poses[i], p2 = truth_poses[i + 1]; glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]); glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]); glEnd(); glColor3f(0.0f, 0.0f, 1.0f); glBegin(GL_LINES); p1 = estimated_poses[i], p2 = estimated_poses[i + 1]; glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]); glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]); glEnd(); } pangolin::FinishFrame(); usleep(5000); // sleep 5 ms }最后运行结果如下:
/home/guoben/Project/SLAM-homework/ch3/draw_trajectory/bin/drawtraj rmse:2.20727

其中,红色轨迹表示真值,蓝色轨迹表示估计值