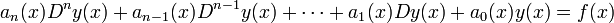线性与非线性

就是变量是一次的就叫做线性，否则就是非线性。
不过每个具体问题都不尽相同。

1. 比如线性函数，就是自变量都是一次的，f(x1,x2,...,xn)=a0+a1x1+a2x2+...+anxn ；

  “线性”与“非线性”，常用于区别函数y = f(x)对自变量x的依赖关系。线性函数即一次函数，其图像为一条直线。其它函数则为非线性函数，其图像不是直线。
　　线性，指量与量之间按比例、成直线的关系，在空间和时间上代表规则和光滑的运动；而非线性则指不按比例、不成直线的关系，代表不规则的运动和突变。

    线性关系是指自变量x与因变量yo之间可以表示成y=ax+b ,（a,b为常数），即说x与y之间成线性关系。不能表示成y=ax+b ,（a,b为常数），即非线性关系，非线性关系可以是二次，三次等函数关系，也可能是没有关系。

2. 线性方程

   线性指的是方程中函数的导数和函数本身都是一次的,但这里仅仅是对于y本身来说,对x没限制.
  也就是说y'+p(x)y+q(x)=0的形式.其中对于p(x)和q(x)并不做限制.
  形式如(y')²+p(x)y+q(x)=0,  y'+p(x)y²+q(x)=0等形式的就不再是线性方程.

3.又比如，

     微分方程：一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。微分方程有时也简称方程。       f(x,y',y'',…``…y(n))=0

   线性微分方程，就是关于各个变量的各阶导数都是一次的，注意是次数是一次，而不是指的一阶导数。y''(x)+y'(x)=0就是线性微分方程，[y'(x)]^2+y'(x)=0就是非线性的。

  具体点说：

      

线性微分方程，是指以下形式的微分方程：

其中微分算子L是线性算子，y是一个未知的函数，等式的右面是一个给定的函数。L是线性的条件，排除了诸如把y的导数平方那样的运算；但允许取y的二阶导数。因此，线性微分方程的一般形式是：

其中D是微分算子d/dx（也就是Dy = y' ，D²y = y"，……），a_i是给定的函数。这个微分方程是n阶的，因为方程中含有y的n阶导数，而不含n+1阶导数。

如果 f(x) = 0，那么方程便称为齐次线性微分方程，它的解称为补函数。这是一种很重要的方程，因为在解非齐次方程时，把对应的齐次方程的补函数加上非齐次方程本身的一个特解，便可以得到非齐次方程的另外一个解。如果a_i 是常数，那么方程便称为常系数线性微分方程。