1330. Reverse Subarray To Maximize Array Value

问题：

给定数组，假定value=数组相邻元素两两之差（绝对值）的总和。

允许对数组内某一个连续子数组进行整体反转，使得value能取得最大。求这样的value。

Example 1:
Input: nums = [2,3,1,5,4]
Output: 10
Explanation: By reversing the subarray [3,1,5] the array becomes [2,5,1,3,4] whose value is 10.

Example 2:
Input: nums = [2,4,9,24,2,1,10]
Output: 68
Explanation: By reversing the subarray [24,2] the array becomes [2,4,9,2,24,1,10] 
whose value is 68.
 
Constraints:
1 <= nums.length <= 3*10^4
-10^5 <= nums[i] <= 10^5

　　

解法：

对于数组：A[0]..., a, [b, ..., c], d, ...A[size-1]

子数组[b, ..., c]反转，对于原数组得到的value的差值为：

原先的两头元素差值，被新的两头元素差值替换

要求的

value = 原先的所有相邻元素差值orig_res + 反转前后的差值reversediff

即可。

接下来，我们讨论，反转前后的差值reversediff的求解：

反转的方式有三种情况：（我们只需在各种情况中取最大的结果即可）

从头开始的左数组：         A[0]~a,b...        ->   a~A[0],b...       ：leftbounddiff 反转前后的差值为：-abs(a-b) + abs(A[0]-b)
以最后元素结束的右数组：...a,b~A[size-1] -> ...a,A[size-1]~b   ：rightbounddiff 反转前后的差值为：-abs(a-b) + abs(a-A[size-1])
中间数组：                     ..., a, b, ..., c , d, ... -> ..., a, c, ..., b , d, ...   ：反转前后的差值为：-(abs(a-b)+abs(c-d)) + (abs(a-c)+abs(b-d))

对于中间数组，我们分以下三种情况，进行讨论：（经过下面的分析，我们最终只选择第3种情况。）

1. [a,b] 和 [c,d] 有相交：

则其reverse前的两头元素差值：如下图红线的和：

reverse后，有两种情况：分别为蓝线和绿线的和，

如下图可知，进行reverse后，红线之和>=蓝线or绿线之和。因此反转并没有使得差值变大。

因此我们不选择将这段[b~c]进行反转。

2. [a,b] 和 [c,d] 有互相包含的关系：

如下图可知，进行reverse后，同样的，红线之和>=蓝线or绿线之和。因此反转并没有使得差值变大。

因此我们不选择将这段[b~c]进行反转。

 

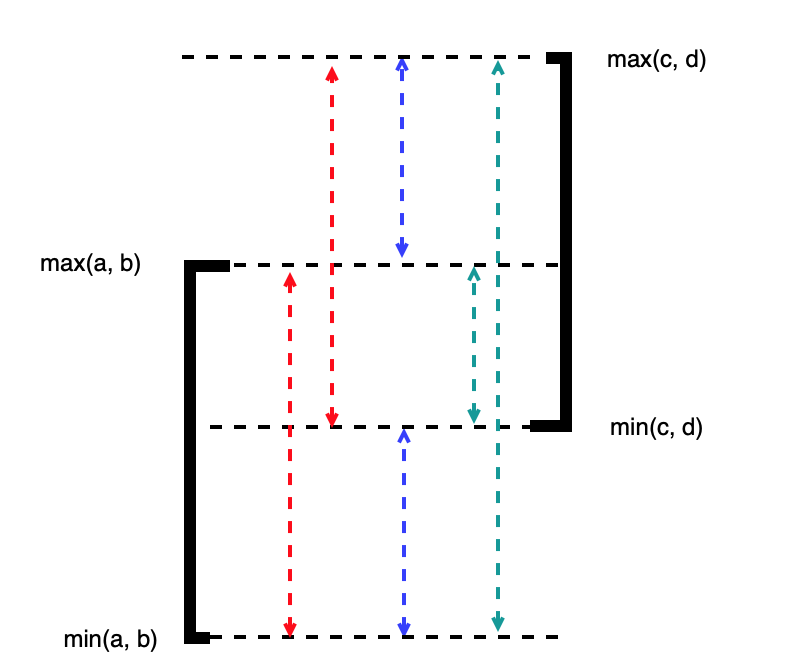
3. [a,b] 和 [c,d] 无相交：

如下图可知，进行reverse后，红线之和<蓝线==绿线之和。

反转，使得差值变大，这正是我们会选择反转的备选之一。

这时，反转前后的差值 = 2 * 黄线

黄线=min(c,d)-max(a,b) = cdlow-abhigh，其中 a和b < c和d

我们要使得反转后的value能取得最大，也就是使得黄线越大。

我们只需要取得a和b最小minabhigh，c和d最大maxcdlow，那么其差值即越大。

 

代码参考：

class Solution {
public:
    int maxValueAfterReverse(vector<int>& nums) {
        int orig_res=0;
        int reversediff=0;
        int maxcdlow=INT_MIN, minabhigh=INT_MAX;
        int leftbounddiff=0, rightbounddiff=0;
        for(int i=0; i<nums.size()-1; i++){
            orig_res+=abs(nums[i]-nums[i+1]);
            
            //为了求最后，中间数组reverse的结果=2*(maxcdlow-minabhigh)
            minabhigh=min(minabhigh, max(nums[i], nums[i+1]));
            maxcdlow=max(maxcdlow, min(nums[i], nums[i+1]));
            
            //左右两边数组reverse的情况：
            leftbounddiff=-abs(nums[i]-nums[i+1])+abs(nums[0]-nums[i+1]);
            rightbounddiff=-abs(nums[i]-nums[i+1])+abs(nums[nums.size()-1]-nums[i]);
            //-(原来的ab之差)+(新的ab之差)
            reversediff=max(reversediff, max(leftbounddiff, rightbounddiff));
            //求reverse改变差值最大的，作为新的reversediff
        }
        reversediff=max(reversediff, 2*(maxcdlow-minabhigh));
        return orig_res+reversediff;
    }
};