1391. Check if There is a Valid Path in a Grid

问题：

给定一个n*m数组，代表公路。

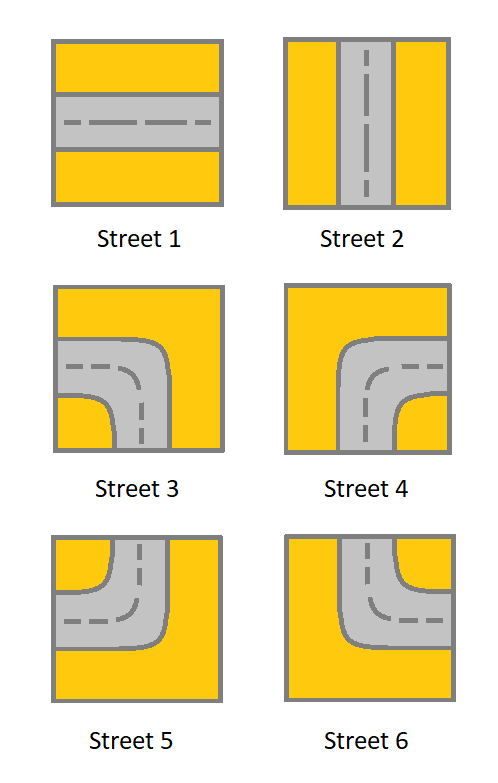
• 1:连接 left + right
• 2:连接 up + down
• 3:连接 left + down
• 4:连接 right + down
• 5:连接 left + up
• 6:连接 right + up

求是否能够从左上角格子(0,0)到达，右下角(n-1,m-1)。

​

Example 1:
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2:
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:
Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Example 4:
Input: grid = [[1,1,1,1,1,1,3]]
Output: true

Example 5:
Input: grid = [[2],[2],[2],[2],[2],[2],[6]]
Output: true
 

Constraints:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
1 <= grid[i][j] <= 6

　　

example 1:

​

example 2:

​

解法：BFS ，Union Find

解法一：BFS：

• 状态：当前位置坐标。
  • visited也标记已访问过的坐标。
• 选择：next=当前格子所连接的两个方向。
  • 除去：next：超出边界 or 已访问过位置 or 当前位置cur：不位于next的连接方向上。
    • op[cur].count(grid[next])==0

代码参考：

class Solution {
public:
    vector<vector<vector<int>>> dir = {{},{{0,-1},{0,1}},{{-1,0},{1,0}},{{0,-1},{1,0}},
                               {{1,0},{0,1}},{{0,-1},{-1,0}},{{-1,0},{0,1}}};
    vector<vector<unordered_set<int>>> opt = {{},{{1,4,6},{1,3,5}},{{2,3,4},{2,5,6}},
                                              {{1,4,6},{2,5,6}},{{2,5,6},{1,3,5}},
                                              {{1,4,6},{2,3,4}},{{2,3,4},{1,3,5}}};
    bool hasValidPath(vector<vector<int>>& grid) {
        int n = grid.size();
        int m = grid[0].size();
        queue<pair<int,int>> q;
        unordered_set<int> visited;//i*300+j
        q.push({0,0});
        visited.insert(0);
        while(!q.empty()) {
            auto[i,j] = q.front();
            q.pop();
            if(i==n-1 && j==m-1) return true;
            for(int k=0; k<2; k++) {//from & to
                auto d = dir[grid[i][j]][k];
                auto op = opt[grid[i][j]][k];
                int x = i+d[0];
                int y = j+d[1];
                //cout<<"x,y:"<<x<<","<<y<<endl;
                if(x<0 || y<0 || x>=n || y>=m || op.count(grid[x][y])==0) continue;
                if(visited.insert(x*300+y).second) {
                    q.push({x,y});
                    //cout<<"push:"<< grid[x][y]<<endl;
                }
            }
        }
        return false;
    }
};

解法二：Union Find

将每个cell的边+cell中心，都看作一个node，

那么每个街道的布局即可看作，将中心和其中两个边 代表的node 相连。

例如：

3:连接 left + down

• 假设中心为(i,j)
• left边为(i,j-1)
• down边为(i+1,j)

布局3则可看作，将上述三个节点相连。

根据题意，对于节点(i,j)

按照上述方法进行标记节点的话，其节点坐标为(i*2,j*2)

那么对于(0,0) 中心节点坐标为（0，0）上边（-1，0）左边（0，-1）

整个地图的上边界和左边界都为-1，而我们只要求中心节点：起始(0,0)~终点((n-1)*2, (m-1)*2)，也用不到-1的节点，因此不计算在内也完全可以。

使用union find方法，

那么共有2n*2m个节点。

构造记录root数组 uf[n][m]

初始化为各自坐标自己。

实现find，merge方法：

class UnionFind {
public:
    vector<vector<int>> uf;
    int m, n;
    UnionFind(int m1, int n1) {
        m=m1, n=n1;
        uf.resize(2*n, vector<int>(2*m));
        for(int i=0; i<2*n; i++) {
            for(int j=0; j<2*m; j++) {
                uf[i][j] = i*600+j;
            }
        }
    }
    int find(int i, int j) {
        if(uf[i][j]!=(i*600+j)) {
            uf[i][j] = find(uf[i][j]/600, uf[i][j]%600);
        }
        return uf[i][j];
    }
    void merge(int i, int j, int x, int y) {
        if(x<0 || y<0 || x>=2*n || y>=2*m) return;
        int ij = find(i,j);//Root(i,j)
        int xy = find(x,y);//Root(x,y)
        if(ij==xy) return;
        uf[xy/600][xy%600] = ij;//connect two root:let uf(Root(x,y))==Root(i,j);
        //cout<<"merge:uf["<<x<<"]["<<y<<"]:"<<ij<<endl;
        return;
    }
};

再利用union find进行对本问题的求解。

对每个cell，根据道路布局，进行节点merge

最后所求即是，起始节点和终点是否为同一个root。

代码参考：

class Solution {
public:
    vector<vector<int>> dir = {{-1,0},{1,0},{0,-1},{0,1}};//edges from center: up,down,left,right
    vector<unordered_set<int>> opt = {{2,5,6},{2,3,4},{1,3,5},{1,4,6}};
    bool hasValidPath(vector<vector<int>>& grid) {
        int n = grid.size();
        int m = grid[0].size();
        UnionFind node(m,n);
        for(int i=0; i<n; i++) {
            for(int j=0; j<m; j++) {
                for(int k=0; k<4; k++) {
                    if(opt[k].count(grid[i][j]))
                        //connect: center + edge
                        //center: 2*i, 2*j
                        node.merge(2*i,2*j, 2*i+dir[k][0], 2*j+dir[k][1]); 
                }
            }
        }
        return node.find(0,0) == node.find(2*n-2, 2*m-2);
    }
};