1.算法运算:
1.1. 获得最低非0位:
1 //获取x的最低1位。 2 //e.g. 6 = 0110 3 //获得 2 = 10 4 // x=0110, -x=(~x+1)=(1001+1)=1010 5 // x&(-x) = 0110 & 1010 = 0010 6 int lowbit(int x) { 7 return x&(-x); 8 }
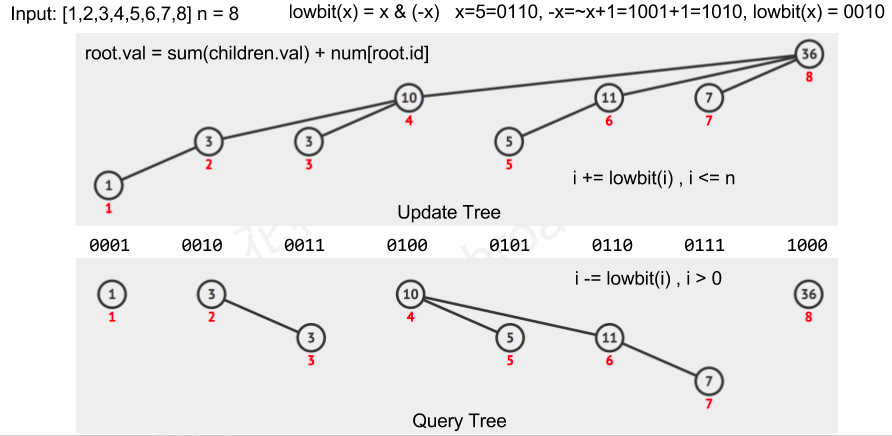
应用:FenwickTree
- updateTree(i)
- ->update(i+lowbit(i)) [until i==tree.size]
- e.g. update(1)-> update(1,10,100,1000...)
- cause: node[10 or 100 or 1000] = sumof(node[1]+...) 这几个节点都包含 i 元素的信息。
- queryTree(i): == get sum(0~i)
- ->val+=queryTree(i-lowbit(i)) [until i==0]
- e.g. query(7)-> query(111, 110, 100)
- cause: Sum(1+...+7) = Sum(7) + Sum(5,6) + Sum(1,2,3,4) = node(111)+node(110)+node(100)
1 class FenwickTree { 2 private: 3 vector<int> partSum; 4 int lowest1bit(int num){ 5 return num & (-num); 6 //-num = ~num+1 7 //e.g. num=5 (0110) -> -num = -5 = ~(0110)+1 = 1001 +1 = 1010 8 // num & (-num) = 0110 & 1010 = 0010 9 } 10 public: 11 FenwickTree(int n):partSum(n+1,0) {} 12 //update all the item in the partition Sum route of i 13 void update(int i, int val){ 14 while(i<partSum.size()){ 15 partSum[i]+=val; 16 i+=lowest1bit(i); 17 } 18 } 19 //find Sum(0~i) 20 int query(int i){ 21 int sum=0; 22 while(i>0){ 23 sum+=partSum[i]; 24 i-=lowest1bit(i); 25 } 26 return sum; 27 } 28 };
1.2. 去掉最低非0位:
1 //消除x的最低1位。 2 //e.g. 6 = 0110 3 //获得 4 = 0100 4 // x=0110, x-1=0101 5 // x&(x-1) = 0110 & 0101 = 0100 6 int rm_lowbit(x) { 7 return x&(x-1); 8 }
应用:
1.2.1. 计算汉明权重(Hamming Weight)
返回x中有几个 1。
== bitset<n>.count()
== __builtin_popcount(unsigned u)
1 int hammingWeight(uint32_t x) { 2 int res = 0; 3 while (x != 0) { 4 x = x & (x - 1); 5 res++; 6 } 7 return res; 8 }
1.2.2. 判断一个数是不是 2 的指数
判断x中是否只有一个 1。
1 bool isPowerOfTwo(int x) { 2 if (x <= 0) return false; 3 return (x & (x - 1)) == 0; 4 }
2. 位运算技巧:
2.1. 异或 ^
应用:
2.1.1. 判断某个数组中,唯一出现奇数次的元素。
- a ^ a = 0
- a ^ 0 = a
1 int singleNumber(vector<int>& nums) { 2 int res = 0; 3 for (int x : nums) { 4 res ^= x; 5 } 6 return res; 7 }
2.1.2. 判断两个数是否异号
- 异号:
- int x = -1, y = 2;
- (x ^ y) < 0
- 同号:
- int x = 3, y = 2;
- (x ^ y) >= 0
2.1.3. 交换两个数:swap(a, b)
1 int a = 1, b = 2; 2 a ^= b; 3 b ^= a; 4 a ^= b; 5 // 现在 a = 2, b = 1
2.1.4. 大小写互换: ^ ' '
1 ('d' ^ ' ') = 'D' 2 ('D' ^ ' ') = 'd'
- Tip:
- 无区别转大写: & '_'
1 ('b' & '_') = 'B' 2 ('B' & '_') = 'B'
-
- 无区别转小写: | ' '
1 ('a' | ' ') = 'a' 2 ('A' | ' ') = 'a'