记录快排相关-快速排序、快速选择Topk。快速排序的优化-Python

关于排序的一些想法

实际上从实用的角度看，排序的那么多分类标准似乎只有复杂度、场景、以及稳定性的对于重应用的程序员比较有意义，除了把所有排序通讲

之外，把比较常出现的能够扩展的排序方法都单独写一个Blog，快排、堆排、二分、以及Timsort

快排实际上就是三个步骤

1. 挑选排序的基准
2. 划分为比基准大小的左右两部分
3. 递归的求解左右子数组

这里其他语言第二步还比较麻烦，把基准的坑腾出来进行划分，Python中可以直接用列表表达式写出来，还是比较简洁的

再说到快排本身  实际上这就是一个递归求解的多叉树，什么时候把所有叶子分清楚了就结束了，如下图

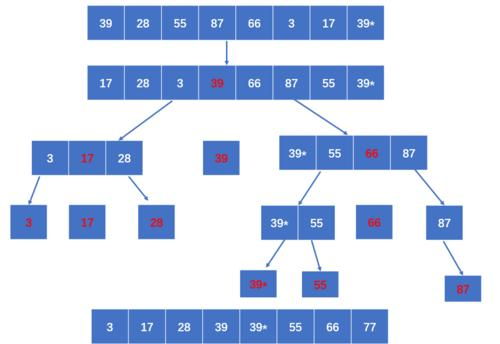
 实际上每一层具体的时间复杂度只可能等于n，时间复杂度完全取决于树高，树高则取决于你的左右子树每层的工作量

比如某一层，左子树只处理了一个数字（也就是只有一个数比基准小），那他就会耽误进度，让递归树变高，甚至退化成链表，

也就是待排序列nums是升序的或者是降序的。

所以最好情况是O(nlogn) 最坏是O(n^2)

关于Topk的快速选择

Topk是一个选出数组中第k大/小的问题

Topk一般排序解法有两种，快选和推排序，这里我们正好说一下快排进化来的快选

快排是每层总是n的工作量，以此在递归树中完成整个数组的排序，而快速选择则不需要，我们只要找出Topk即可，也就是左右数组我们只留一个

[7,2,14,4,6,8,12,19],要找第3个也就是6

这时候比如以7为基准，[2,4,6]  [14,8,12,19]快排需要左右都完成，而快选是只要左边就可以，因为len（left）>= k也就是3，右边不需要了，

所以复杂度是O(n+n/2+n/4...+1)实际上还是On

关于快速排序的优化

实际上快排效率差的大多两种情况

　　1.升序降序序列

　　2.重复值

　　3.小数组快排效率不如插入

针对这些情况有以下几种优化方案

1.随机化选择基准

这个计算机算法设计与分析这本书上讲过几种随机化算法，随机选择基准来消除总是选择num[0]带来的升序降序数组退化成On^2的情况

但实际上消除不了，而是大大降低了这种概率 

2.三数取中选择基准

这样基本消除了升降序的问题

3.当快排进行到一定大小，改用插入排序）

4.额外处理相同元素，【1，22，3，3，3，5，7，8】比如宣到3为基准，其实会影响效率，而当全部都是3时，效率会急剧下降，所以对与基准重复的数字不再放入左右数组

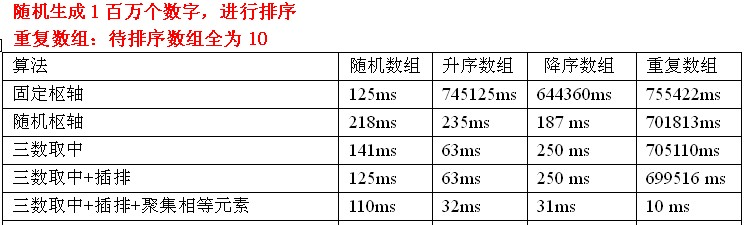
 这是一张效率图，参考自https://blog.csdn.net/insistgogo/article/details/7785038

里面有各种版本的代码，有兴趣的同学可以看看