luogu 1375 小猫 （卡特兰数）

这是我做题史上摔得最惨的一道黄题，15条记录转眼化为泪水。o(╥﹏╥)o

这道题目从10.12开始尝试，随机跳题跳到了这题，一看就是卡特兰数，因为样例太像了。。

然后小心证明

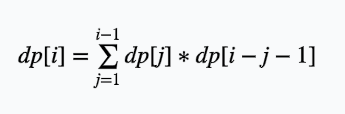
这个就是catalan的式子啊，，

然后打了一发阶乘+逆元求组合数再套公式，

ll fac[N], inv[N], fi[N] ;

void init() {
    fac[0] = fac[1] = inv[0] = inv[1] = fi[0] = fi[1] = 1 ;
    for (int i = 2; i < N; i++) {
        fac[i] = fac[i - 1] * i % MOD ;
        inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD ;
        fi[i] = inv[i] * fi[i - 1] % MOD;
    }
}

ll C(ll a, ll b){
    return fac[a] * fi[b] % MOD * fi[a - b] % MOD;
}

int n ; 

int main(){    
    init() ;
    scanf("%d", &n) ;
    printf("%lld
", C(2 * n, n) / (n + 1)) ;
}

30，就是跟暴力一样。。。

然后之后暴力改了改，还是30

于是先把暴力的$O(n^2)dp$敲了，拿了60分

开大数组，80分，TLE两个点，一想，肯定是暴力的顶峰了，。

#include<cstdio>
#include<cstdlib>
long long c[100010]={1,1,2};
int main(){
    int n,i,j;
    scanf("%d",&n);
    for(i=3;i<=n;i++){
        j=0;
        while(j<=i-1){
            c[i]+=c[j]*c[i-1-j];
            while(c[i]>=1000000007) c[i]%=1000000007;
            j++;
        }
    }
    printf("%lld",c[n]);
}

之后这个题目就再没碰过，直到today，11.29

发现第一个30分代码没有强转ll，改了一下，30。

发现输出答案直接除，应该转为逆元，60了

之后觉得预处理麻烦，干脆不用，60。。

放一下60分代码

int jc(int a) {
    if (a == 1) return 1 ;
    else return 1ll * a * jc(a - 1) % MOD ;
}

int power(int a, int b) {
    int res = 1 ;
    for (; b >>= 1; a = 1ll * a * a % MOD) if (b & 1) res = 1ll * res * a % MOD ;
    return res ;
}

int C(int a, int b){
    return 1ll * jc(a) * power(jc(b), MOD - 2) % MOD * power(jc(a - b), MOD - 2) % MOD;
}

int n ;

int main(){
    scanf("%d", &n) ;
    printf("%lld
", 1ll * C(2 * n, n) * power(n + 1, MOD - 2) % MOD) ;
}

发现自己C里面b和a-b没套jc，尴尬了

改完，依然60

冷静分析，发现自己快速幂写错了，自闭了。。

我怎么那么菜啊，。。。

然后就AC了

放一下最终代码：

#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <vector>
#include <bitset>
#include <cstdio>
#include <cctype>
#include <string>
#include <cstring>
#include <cassert>
#include <climits>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std ;
#define int long long
#define rep(i, a, b) for (int (i)=(a);(i)<=(b);(i)++)
#define Rep(i, a, b) for (int (i)=(a)-1;(i)<(b);(i)++)
#define REP(i, a, b) for (int (i)=(a);(i)>=(b);(i)--)
#define reg(i, x) for (int (i)=head[x];(i);i=e[i].next)
#define clr(a) memset(a,0,sizeof(a))
#define Sort(a, len) sort(a + 1, a + len + 1)
#define Sort2(a, len, cmp) sort(a + 1, a + len + 1, cmp)
#define ass(a, sum) memset(a, sum, sizeof(a))

#define ull unsigned long long
#define ll long long
#define ls ((rt) << 1)
#define rs ((rt) << 1 | 1)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define endl '
'
#define Pii pair<int, int>

const int N = 100010 ;
const int iinf = INT_MAX/2 ;
const ll linf = LLONG_MAX/2 ;
const int MOD = 1e9 + 7 ;

inline int read(){
    int X = 0,w = 0 ;
    char ch = 0;
    while(!isdigit(ch)) {w |= ch == '-';ch = getchar();}
    while(isdigit(ch)) X = (X<<3) + (X<<1) + (ch ^ 48),ch = getchar();
    return w ? -X : X;
}

void write(int x){
     if(x < 0) putchar('-'),x = -x;
     if(x > 9) write(x / 10);
     putchar(x%10 + '0');
}

int jc(int a) {
    if (a == 1) return 1 ;
    else return 1ll * a * jc(a - 1) % MOD ;
}

int power(int a, int b) {
    int res = 1 ;
    for (; b; b >>= 1, a = 1ll * a * a % MOD) if (b & 1) res = 1ll * res * a % MOD ;
    return res ;
}

int C(int a, int b){
    return 1ll * jc(a) * power(jc(b), MOD - 2) % MOD * power(jc(a - b), MOD - 2) % MOD;
}

int n ;

signed main(){
    scanf("%lld", &n) ;
    printf("%lld
", 1ll * C(2 * n, n) * power(n + 1, MOD - 2) % MOD) ;
}

/*
写代码时请注意：
    1.是否要开Long Long？数组边界处理好了么？
    2.特殊情况处理好了么？
    3.做一些总比不做好。
    4.最大值和最小值问题可不可以用二分答案？
    5.有没有贪心策略？否则能不能dp？
    6.实数精度有没有处理？
*/