奇安信前端算法笔试(2021秋招)——动态规划

1.背景

　　就在前天，我去参加了奇安信前端招聘的笔试，在考核的算法题中，有一道题就是动态规划，毫无准备的我当场放弃，笔试后，赶紧查资料，写下这篇博客，回顾这类问题的解决方法。

2.问题引入

　　原题题意大概是这样的：8*8的棋盘上面放着64个不同价值的礼物，每个小的棋盘上面放置一个礼物（礼物的价值大于0），一个人初始位置在棋盘的左上角，每次他只能向下或向右移动一步，并拿走对应棋盘上的礼物，结束位置在棋盘的右下角，请设计一个算法使其能够获得最大价值的礼物。

　　参考博客地址：https://www.cnblogs.com/luxiaoxun/archive/2012/11/15/2771605.html，对应其中第4题，原文C++代码如下： 

int GetMaxValue(int **dp, int **value)
{
    int i, j, n = 8;  
    dp[0][0] = value[0][0];  
    for(i = 1; i < n; i++)  
    {  
        dp[i][0] = dp[i-1][0] + value[i][0];  
    }  
    for(j = 1; j < n; j++)  
    {  
        dp[0][j] = dp[0][j-1] + value[0][j];  
    }  

    for(i = 1; i < n; i++)  
    {  
        for(j = 1; j < n; j++)  
        {  
            dp[i][j] = max(dp[i][j-1] , dp[i-1][j]) + value[i][j];  
        }  
    }  
    return dp[n-1][n-1];
}

3.解决方法

　　这段代码没有任何注释，咋一看一头雾水，凭借我只学过C语言的基础，仔细看，仔细研究，最终搞懂了这精妙的算法。

动态规划算法：  
dp[i][j] 表示到棋盘位置（i，j）上可以得到的最大礼物值  
dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) + value[i][j]  （0<i，j<n）

　　GetMaxValue方法传入了两个参数，dp和value。其中value是一个存储n*n棋盘上各个位置礼物价值的二维数组，而dp是一个存储行走到棋盘该位置所能够获得最大礼物价值的二维数组。

　　在方法中，首先初始化了第一个位置(0, 0)所能够获得的最大礼物价值，当然就是(0, 0)当前位置礼物的价值。

　　接着是两个循环，分别给出了走到棋盘的第一列和第一行所有元素能获取礼物的最大价值(因为如果走到该位置，那么一定是一直往右走或者一直往下走)。

　　最后，有了前面的基础，通过循环遍历就能得到剩余位置所能得到礼物的最大价值，最终返回dp数组(7, 7)位置处的值就是整个棋盘从(0, 0)走到(7, 7)所能得到礼物的最大价值。用图简单说明如下： 

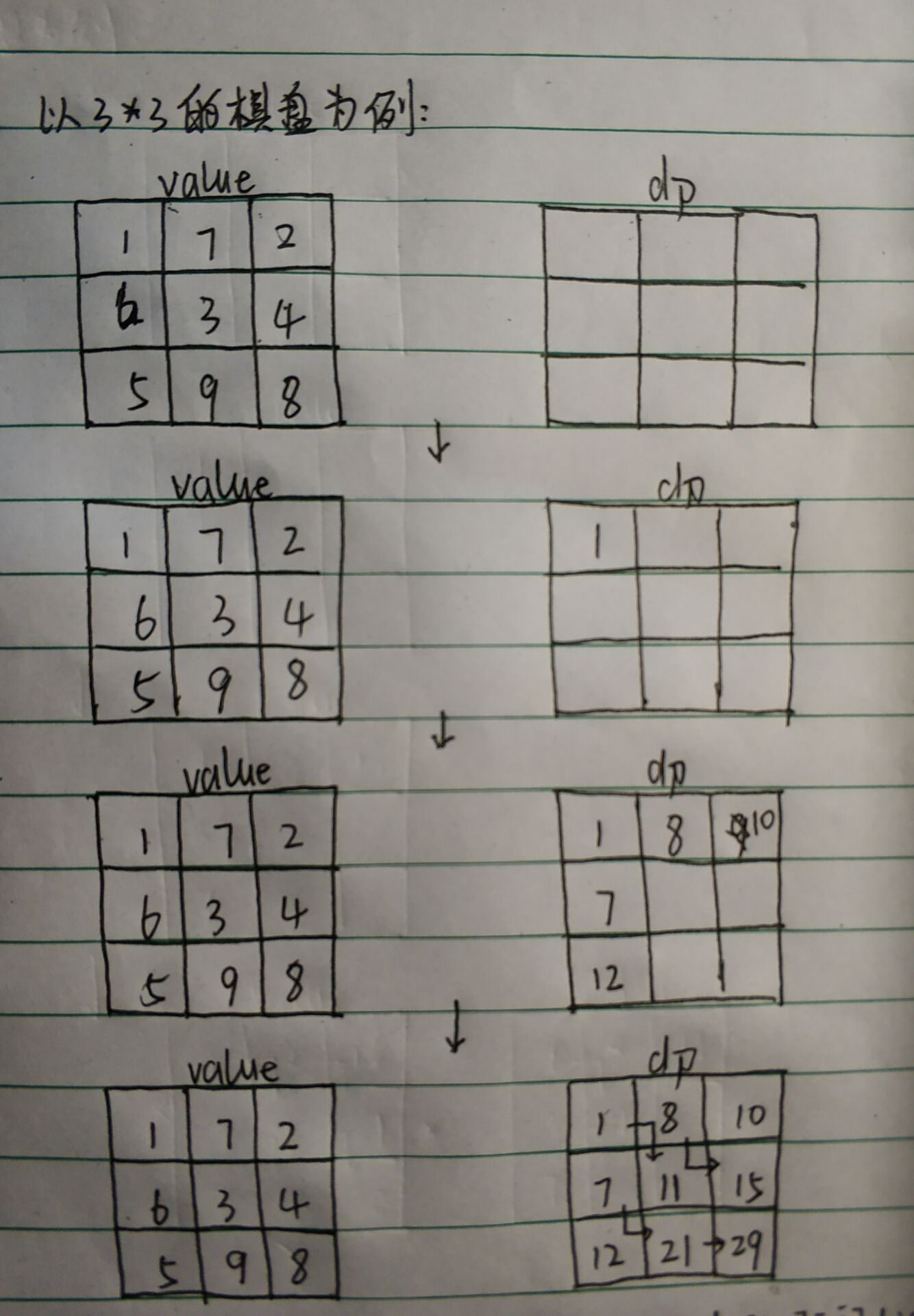
　　JS代码如下：

/**
 * @param {Array} valueArr 存储棋盘各个位置的礼物价值
 * @param {Array} resArr 存储从棋盘左上角到达棋盘各个位置所能获得的最大礼物价值
 */
const getMaxValue = (valueArr, resArr) => {
    const n = 8
    // 初始化左上角的res
    resArr[0][0] = valueArr[0][0]
    // 初始化第一列的res
    for (let i = 1; i < n; i++) {
        resArr[i][0] = resArr[i - 1][0] + valueArr[i][0]
    }
    // 初始化第一行的res
    for (let j = 1; j < n; j++) {
        resArr[0][j] = resArr[0][j - 1] + valueArr[0][j]
    }
    // 通过前面的基础，求出棋盘剩余位置所能获得的最大礼物价值                
    for (let i = 1; i < n; i++) {
        for (let j = 1; j < n; j++) {
            resArr[i][j] = Math.max(resArr[i - 1][j], resArr[i][j - 1]) + valueArr[i][j]
        }
    }

    return resArr[n - 1][n - 1]
}

4.参考博客

　　https://www.cnblogs.com/luxiaoxun/archive/2012/11/15/2771605.html