分治FFT
前置问题:如何对任意已知f,g,l<=r,l1<=r1,对于所有$l1<=k<=r1$,求$sum_{i=l}^rf_ig_j[i+j=k]$(①)?
答案:
设$f'_i=f_{i+l}$,$k'=k-l$则$l1-l<=k'<=r1-l$
①式$=sum_{i=0}^{r-l}f'_ig_j[i+j=k']$
设$g'_i=g_{i+l1-r}$,$k''=k'-l1+r$则$r-l<=k''<=r1-l1+r-l$
①式$=sum_{i=0}^{r-l}f'_ig'_{j-l1+r}[i+j-l1+r=k'']$
$=sum_{i=0}^{r-l}f'_ig'_j[i+j=k'']$
把$f'$的第r-l之后的项都赋值为0,然后对$f'$和$g'$卷积就可以了,取出结果中第r-l到r1-l1+r-l项作为答案即可。注意到只需要f的第l到r项,g的第l1-r到r1-l项,卷积结果的第r-l到r1-l1+r-l项(当然实际上只能把0到r1-l1+r-l项都算出来),因此复杂度O((r1-l1+r-l)log(r1-l1+r-l))
上面的推导好像有点迷,当初我应该是用了一点数形结合(?)的思想
首先给一张矩形表格,行是i,表示f数列,列是j,表示g数列,每一个格子上的值就是f[i]*g[j]
以下的示意图中,画一条线表示要求这一条线上所有格子的和(可能会画偏;在此题中都是表示一条对角线上格子的和);示意图用excel画的,因此列(j)用A,B,C,D,..表示
首先,FFT直接能求的长这样: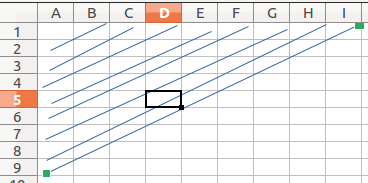
一开始要求的大概是这样:
第一步可以把这个东西向上平移l格,相当于设了f'和k',大概变成这样:

第二步可以把这个东西向左平移l1-r格,相当于设了g'和k'',大概变成这样:
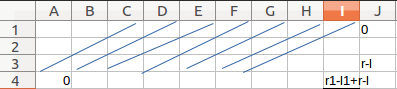
这时下一步做法就很明显了,把f'超过r-l的项全部设为0,然后f'和g'卷积,并取出结果中第r-l到r1-l1+r-l项
此题:$f_k=sum_{i=0}^{k-1}f_ig_{k-i}$;$f_0=1$
考虑分治。各个序列中不存在的项全部当成是0
solve(l,r):在l左边的f值,以及对于所有$l<=k<=r$,$sum_{i=0}^{l-1}f_ig_{k-i}$,都已经正确求出来时,求出f[l]到f[r]的值。
先solve(l,mid),再计算[l,mid]对[mid+1,r]的贡献,再solve(mid+1,r)
计算[l,mid]对[mid+1,r]的贡献,就相当于要对于所有$mid+1<=k<=r$,计算$sum_{i=l}^{mid}f_ig_j[i+j=k]$
用上面的方法完成即可
附:这题里面,快读快写基本没用;可以一开始就把n处理成2的幂,常数也许会更小(?);小范围暴力有用,以下代码大概在开O2以后开到r-l<=K,K在100到200左右时进行暴力比较合适(大概是FFT常数真的大吧...)
版本1:

1 #pragm 2 a GCC optimize(2) 3 #include<cstdio> 4 #include<algorithm> 5 #include<cstring> 6 #include<vector> 7 using namespace std; 8 #define fi first 9 #define se second 10 #define mp make_pair 11 #define pb push_back 12 typedef long long ll; 13 typedef unsigned long long ull; 14 15 const ll md=998244353; 16 ll poww(ll a,ll b) 17 { 18 ll base=a,ans=1; 19 for(;b;b>>=1,base=base*base%md) 20 if(b&1) 21 ans=ans*base%md; 22 return ans; 23 } 24 const int N=131073; 25 int n,n1;ll g[N],f[N],t1[N],t2[N]; 26 int rev[N]; 27 void init(int len) 28 { 29 int bit=0,i; 30 while((1<<(bit+1))<=len) ++bit; 31 for(i=0;i<len;++i) 32 rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1)); 33 } 34 void dft(ll *a,int len,int idx) 35 { 36 int i,j,k;ll wn,wnk,t1,t2; 37 for(i=0;i<len;++i) 38 if(i<rev[i]) 39 swap(a[i],a[rev[i]]); 40 for(i=1;i<len;i<<=1) 41 { 42 wn=poww(idx==1?3:332748118,(md-1)/(i<<1)); 43 for(j=0;j<len;j+=(i<<1)) 44 { 45 wnk=1; 46 for(k=j;k<j+i;++k,wnk=wnk*wn%md) 47 { 48 t1=a[k];t2=a[k+i]*wnk%md; 49 a[k]+=t2;a[k+i]=t1-t2; 50 (a[k]>=md) && (a[k]-=md); 51 (a[k+i]<0) && (a[k+i]+=md); 52 } 53 } 54 } 55 if(idx==-1) 56 { 57 ll ilen=poww(len,md-2); 58 for(i=0;i<len;++i) 59 (a[i]*=ilen)%=md; 60 } 61 } 62 void solve(int l,int r) 63 { 64 int i,j; 65 if(r-l<=128) 66 { 67 for(i=l;i<=r;++i) 68 { 69 for(j=l;j<i;++j) 70 { 71 (f[i]+=f[j]*g[i-j])%=md; 72 } 73 } 74 return; 75 } 76 int mid=(l+r)>>1,len=r-l+1; 77 solve(l,mid); 78 memcpy(t1,f+l,sizeof(ll)*(mid-l+1)); 79 memcpy(t2,g+1,sizeof(ll)*(r-l)); 80 memset(t1+mid-l+1,0,sizeof(ll)*(r-mid)); 81 init(len); 82 dft(t1,len,1); 83 dft(t2,len,1); 84 for(i=0;i<len;++i) 85 (t1[i]*=t2[i])%=md; 86 dft(t1,len,-1); 87 for(i=mid+1;i<=r;++i) 88 { 89 f[i]+=t1[i-1-l]; 90 (f[i]>=md) && (f[i]-=md); 91 } 92 solve(mid+1,r); 93 } 94 int main() 95 { 96 int i,t; 97 scanf("%d",&n);n1=n; 98 for(i=1;i<n;++i) 99 scanf("%lld",g+i); 100 for(t=1;t<n;t<<=1); 101 n=t; 102 f[0]=1; 103 solve(0,n-1); 104 for(i=0;i<=n1-1;++i) 105 printf("%lld ",f[i]); 106 return 0; 107 }
多项式求逆
设$F(x)=sum_{i=0}^{+infty}f_ix^i$,$G(x)=sum_{i=0}^{+infty}g_ix^i$
$F(x)G(x)=sum_{i=0}^{+infty}x^isum_{j=0}^if_jg_{i-j}$
$=sum_{i=1}^{+infty}x^isum_{j=0}^if_jg_{i-j}+x^0f_0g_0$
$=sum_{i=1}^{+infty}x^i(sum_{j=0}^{i-1}f_jg_{i-j}+f_ig_0)+g_0$
$=sum_{i=1}^{+infty}x^i(f_i+f_ig_0)+g_0$
$=(g_0+1)sum_{i=1}^{+infty}x^if_i+g_0$
$=(g_0+1)(sum_{i=0}^{+infty}x^if_i-x^0f_0)+g_0$
$=(g_0+1)(F(x)-1)+g_0$
$=(g_0+1)F(x)-1$
所以$(g_0+1-G(x))F(x)=1$
所以$F(x)equivfrac{1}{g_0-G(x)+1}(mod x^n)$
版本2:基于版本1

1 #prag 2 ma GCC optimize(2) 3 #include<cstdio> 4 #include<algorithm> 5 #include<cstring> 6 #include<vector> 7 #include<cmath> 8 using namespace std; 9 #define fi first 10 #define se second 11 #define mp make_pair 12 #define pb push_back 13 typedef long long ll; 14 typedef unsigned long long ull; 15 const int md=998244353; 16 const int N=2097152; 17 int rev[N]; 18 void init(int len) 19 { 20 int bit=0,i; 21 while((1<<(bit+1))<=len) ++bit; 22 for(i=0;i<len;++i) 23 rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1)); 24 } 25 ll poww(ll a,ll b) 26 { 27 ll base=a,ans=1; 28 for(;b;b>>=1,base=base*base%md) 29 if(b&1) 30 ans=ans*base%md; 31 return ans; 32 } 33 void dft(int *a,int len,int idx)//要求len为2的幂 34 { 35 int i,j,k,t1,t2;ll wn,wnk; 36 for(i=0;i<len;++i) 37 if(i<rev[i]) 38 swap(a[i],a[rev[i]]); 39 for(i=1;i<len;i<<=1) 40 { 41 wn=poww(idx==1?3:332748118,(md-1)/(i<<1)); 42 for(j=0;j<len;j+=(i<<1)) 43 { 44 wnk=1; 45 for(k=j;k<j+i;++k,wnk=wnk*wn%md) 46 { 47 t1=a[k];t2=a[k+i]*wnk%md; 48 a[k]+=t2; 49 (a[k]>=md) && (a[k]-=md); 50 a[k+i]=t1-t2; 51 (a[k+i]<0) && (a[k+i]+=md); 52 } 53 } 54 } 55 if(idx==-1) 56 { 57 ll ilen=poww(len,md-2); 58 for(i=0;i<len;++i) 59 a[i]=a[i]*ilen%md; 60 } 61 } 62 int f[N],g[N],t1[N]; 63 int n,n1; 64 void p_inv(int *f,int *g,int len)//g=f^(-1);f,g长度不小于2^(ceil(log2(len))+1) 65 { 66 g[0]=poww(f[0],md-2); 67 for(int i=2,j;i<(len<<1);i<<=1) 68 { 69 init(i<<1); 70 memcpy(t1,f,sizeof(int)*i); 71 memset(t1+i,0,sizeof(int)*i); 72 memset(g+(i>>1),0,sizeof(int)*(i+(i>>1))); 73 dft(t1,i<<1,1);dft(g,i<<1,1); 74 for(j=0;j<(i<<1);++j) 75 g[j]=ll(g[j])*(2+ll(md-g[j])*t1[j]%md)%md; 76 dft(g,i<<1,-1); 77 } 78 } 79 int main() 80 { 81 int i,t; 82 scanf("%d",&n);n1=n; 83 for(i=1;i<n;++i) 84 scanf("%d",g+i),g[i]=md-g[i]; 85 g[0]=1; 86 for(t=1;t<n;t<<=1); 87 n=t; 88 p_inv(g,f,n); 89 for(i=0;i<n1;++i) 90 printf("%d ",f[i]); 91 return 0; 92 }
