题意:
有n种化学物质,第i种物质现有bi千克,需要ai千克。有n-1种,编号为2-n的转换方式,每种都为(x,k),第i行是编号为i+1的转换方式,编号为i的转换方式(xi,ki)表示ki千克的xi物质可以转换成1千克的i物质,1千克的i物质可以转换成1千克的xi物质。问是否可能通过转换得到足够的需要的物质。(1 ≤ xj + 1 ≤ j)
重点:上面标红的条件。如果只保留ki千克的xi物质可以转换成1千克的i物质产生的一条有向边,表明xi物质连出的边一定是指向编号大于i的物质的(x[i+1]<=i,x[i]<=i-1,x[i]<i),而又恰好有n-1条边,也就是这种情况下这是一棵树。
方法:建树,dfs自底向上递推(我用的方法是只保留ki千克的xi物质可以转换成1千克的i物质产生的一条xi->i的有向边),如果某样物质不够就从父结点那儿转换,如果某样物质多了就把多的转换成父结点的物质。(如果父结点的物质不够,直接减就行,减成负数也没关系)
奇怪的地方:貌似这道题极限数据会爆longlong,然后直接在爆longlong的时候判为NO就行?
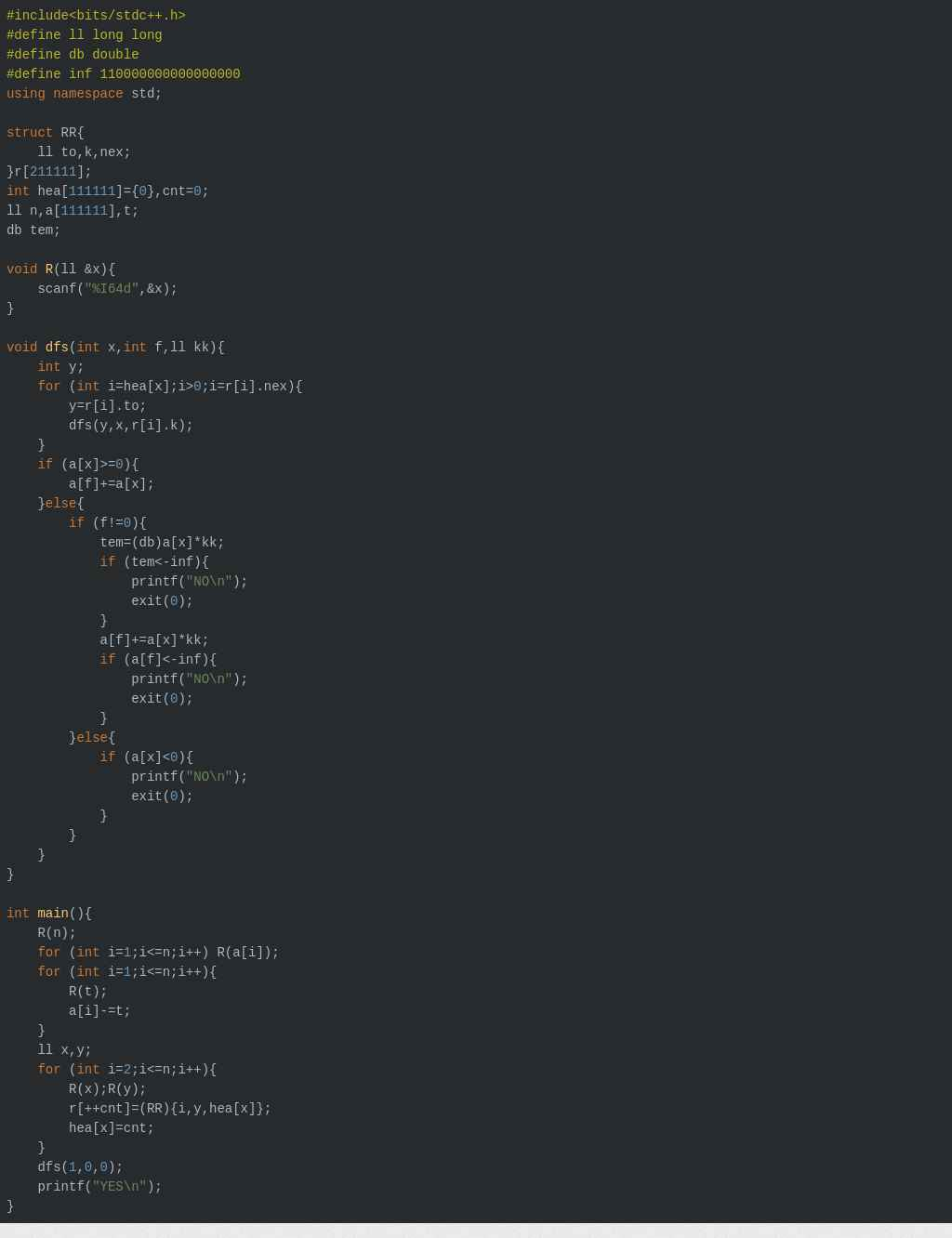
1 #include<cstdio> 2 #include<cstdlib> 3 #define inf 110000000000000000 4 typedef long long LL; 5 struct Edge 6 { 7 LL to,dis,next; 8 }edge[100100]; 9 LL n,num_edge; 10 LL first1[100100]; 11 LL a[100100],b[100100]; 12 double tem; 13 void dfs(LL x,LL fa,LL p) 14 { 15 LL k=first1[x]; 16 while(k!=0) 17 { 18 dfs(edge[k].to,x,edge[k].dis); 19 k=edge[k].next; 20 } 21 // if(a[x]<b[x]) 22 // b[fa]+=b[x]-a[x]; 23 // else if(a[x]>b[x]) 24 // b[fa]-=p*(a[x]-b[x]); 25 if(a[x]<b[x]) 26 b[fa]+=b[x]-a[x]; 27 else if(a[x]>b[x]) 28 { 29 tem=(double)(b[x]-a[x])*p;//为何要double? 30 if(tem<-inf) 31 { 32 printf("NO"); 33 exit(0); 34 } 35 b[fa]-=p*(a[x]-b[x]); 36 if(b[fa]<-inf) 37 { 38 printf("NO"); 39 exit(0); 40 } 41 } 42 } 43 int main() 44 { 45 LL i,x,k; 46 scanf("%lld",&n); 47 for(i=1;i<=n;i++) 48 scanf("%lld",&b[i]); 49 for(i=1;i<=n;i++) 50 scanf("%lld",&a[i]); 51 for(i=2;i<=n;i++) 52 { 53 scanf("%lld%lld",&x,&k); 54 edge[++num_edge].to=i; 55 edge[num_edge].dis=k; 56 edge[num_edge].next=first1[x]; 57 first1[x]=num_edge; 58 } 59 k=first1[1]; 60 while(k!=0) 61 { 62 dfs(edge[k].to,1,edge[k].dis); 63 k=edge[k].next; 64 } 65 if(b[1]<a[1]) 66 printf("NO"); 67 else 68 printf("YES"); 69 return 0; 70 }