二元正态分布可视化本体
由于近来一直再看kaggle的入门书(sklearn入门手册的感觉233),感觉对机器学习的理解加深了不少(实际上就只是调包能力加强了),联想到假期在python科学计算上也算是进行了一些尝试学习,觉得还是需要学习一下机器学习原理的,所以重新啃起了吴恩达的cs229,上次(5月份的时候?)就是在多元高斯分布这里吃的瘪,看不下去了,这次觉定稳扎稳打,不求速度多实践实践,尽量理解数学原理,所以再次看到这部分时决定把这个分布复现出来,吴恩达大佬用的matlab,我用的python,画的还不错,代码如下,
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib as mpl
num = 200
l = np.linspace(-5,5,num)
X, Y =np.meshgrid(l, l)
u = np.array([0, 0])
o = np.array([[1, 0.5],
[0.5, 1]])
pos = np.concatenate((np.expand_dims(X,axis=2),np.expand_dims(Y,axis=2)),axis=2)
a = (pos-u).dot(np.linalg.inv(o))
b = np.expand_dims(pos-u,axis=3)
Z = np.zeros((num,num), dtype=np.float32)
for i in range(num):
Z[i] = [np.dot(a[i,j],b[i,j]) for j in range(num)]
Z = np.exp(Z*(-0.5))/(2*np.pi*np.linalg.det(o))
fig = plt.figure()
ax = fig.add_subplot(111,projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, alpha=0.3, cmap=cm.coolwarm)
cset = ax.contour(X,Y,Z,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-5,cmap=mpl.cm.winter)
cset = ax.contour(X, Y, Z, zdir='y', offset= 5,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr # 蓝,白,红
cm.coolwarm
'''
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
实际操作中,可以看到我在Z生成部分使用了双层循环,我本意是使用numpy广播机制优化掉循环,实际操作不太顺利,(20,20,2)去叉乘(20,20,2,1),结果shape不是我期望的(20,20,1),而是(20,20,20,20,1),也就是说在高维叉乘时其实广播机制不太好用,毕竟实际上两个不同维度矩阵是可以直接叉乘的(虽然对维度有要求),这一点值得注意(高维矩阵叉乘不要依赖numpy的广播机制)。
参数:
u = np.array([0, 0])
o = np.array([[1, 0.5],
[0.5, 1]])

参数:
u = np.array([1, 1])
o = np.array([[1, 0],
[0, 1]])
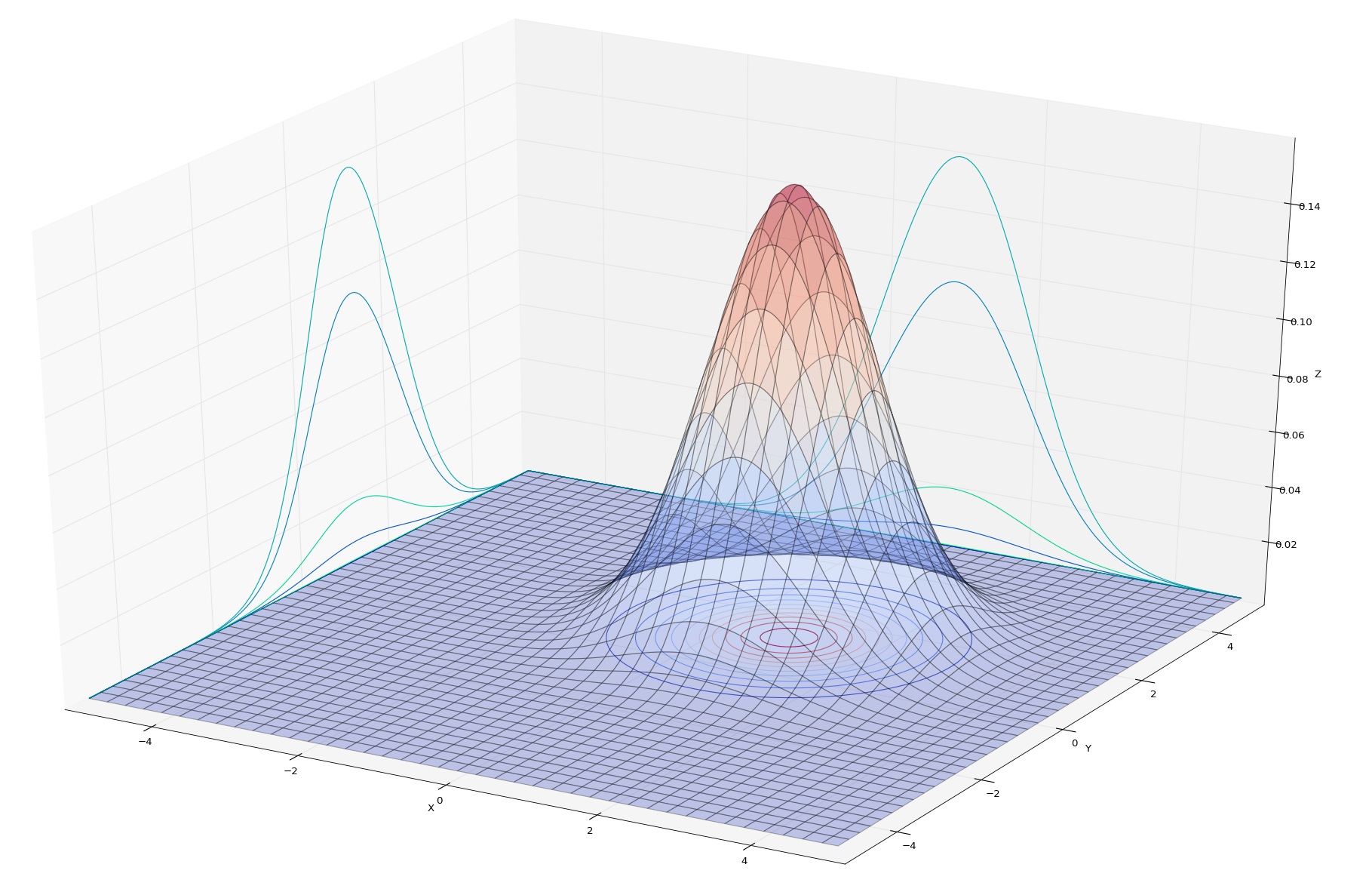
参数:
u = np.array([1, 1])
o = 3*np.array([[1, 0],
[0, 1]])
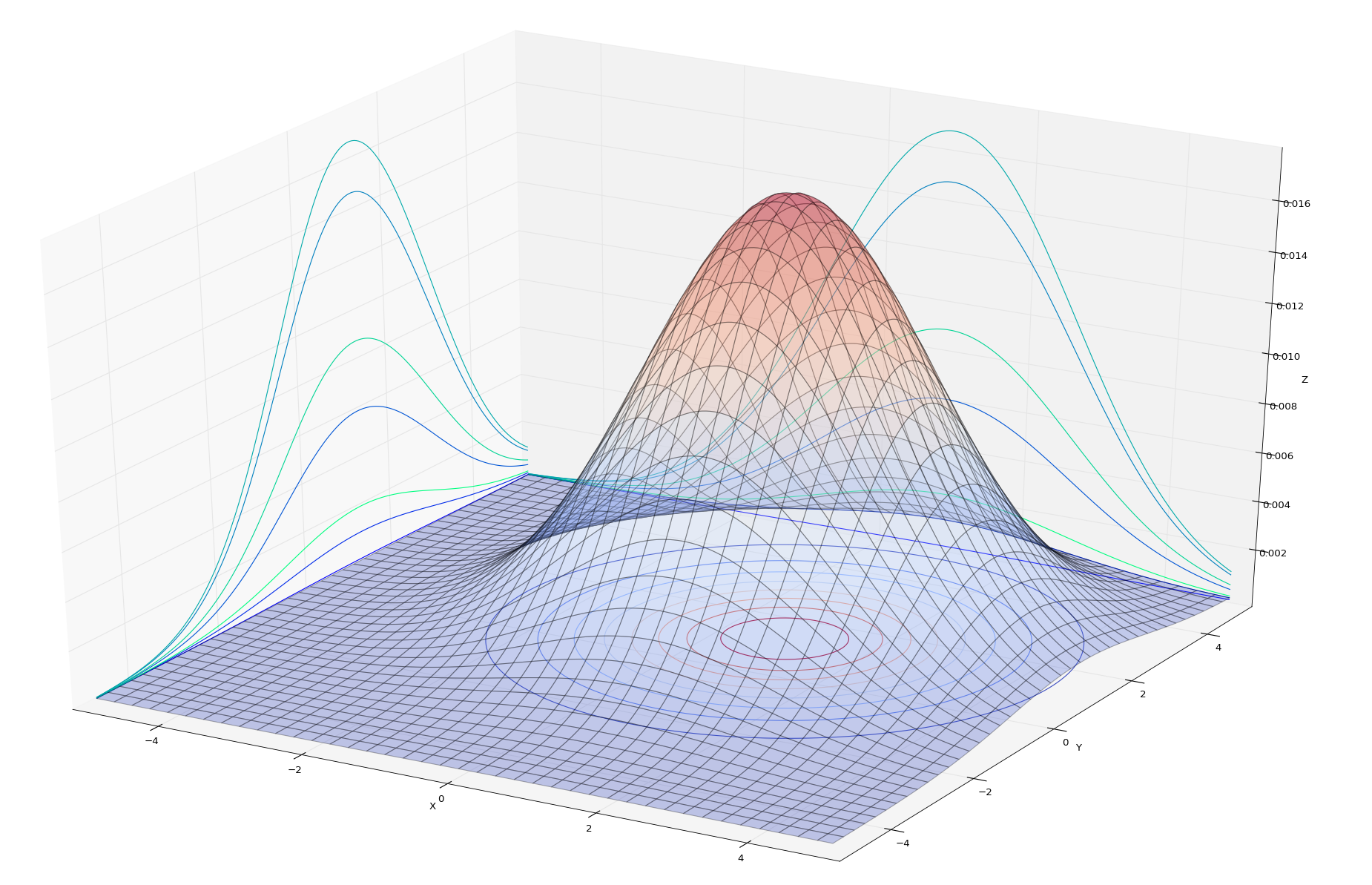
等高线图添加
我们单独绘制一下等高线图,
# 前面添加图的位置修改如下, # ax = fig.add_subplot(211,projection='3d') ax2 = fig.add_subplot(212) cs = ax2.contour(X,Y,Z) ax2.clabel(cs, inline=1, fontsize=20)
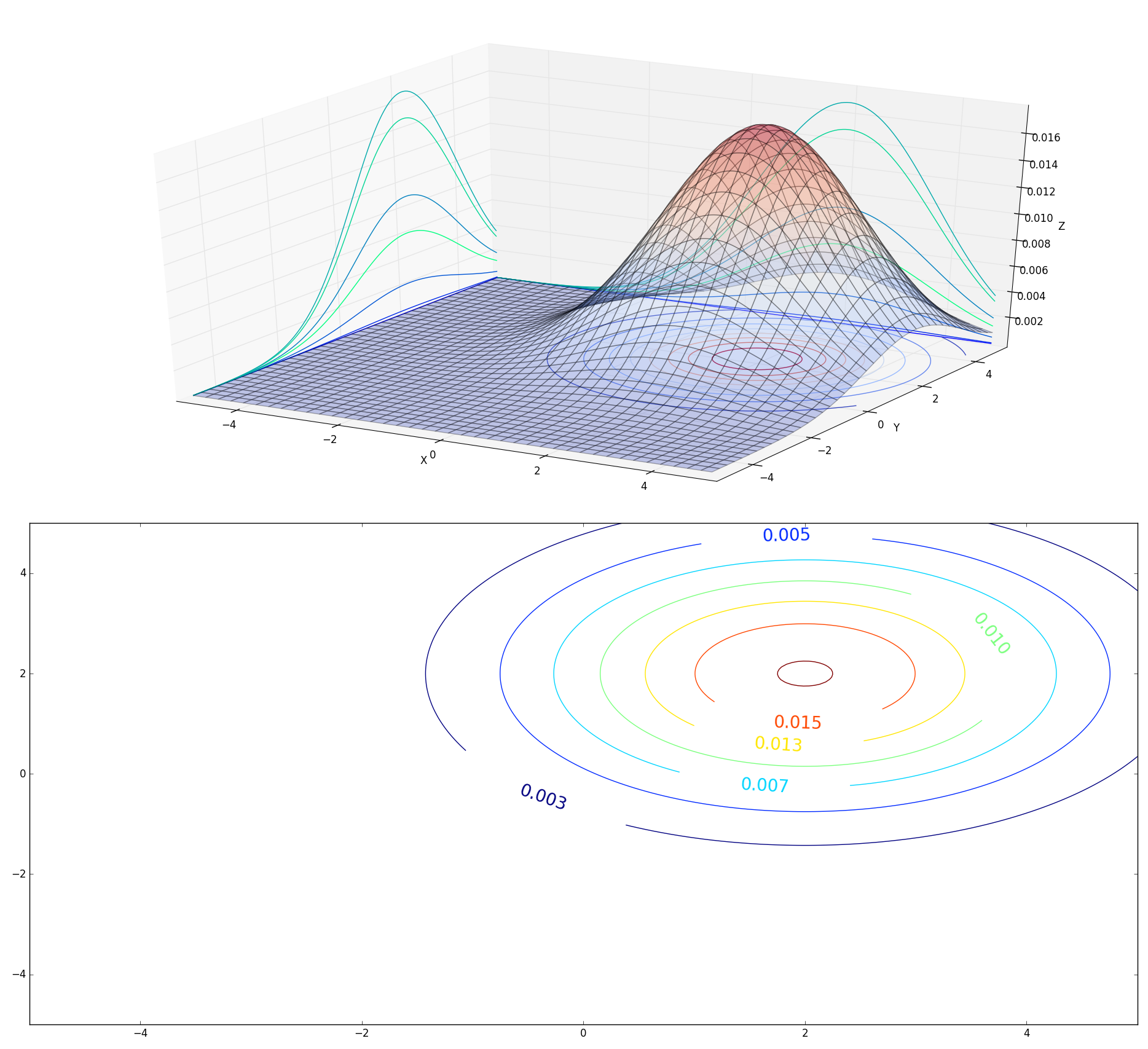
高斯判别分析模型示意图可视化
现在我们在上面代码的基础上可视化吴恩达老大的下一节的图,高斯判别分析模型可视化,这里面我们仅仅可视化基础的双高斯独立分布,代码如下,
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib as mpl
num = 200
l = np.linspace(-5,5,num)
X, Y =np.meshgrid(l, l)
pos = np.concatenate((np.expand_dims(X,axis=2),np.expand_dims(Y,axis=2)),axis=2)
u1 = np.array([2, 2])
o1 = 3*np.array([[1, 0],
[0, 1]])
a1 = (pos-u1).dot(np.linalg.inv(o1))
b1 = np.expand_dims(pos-u1,axis=3)
Z1 = np.zeros((num,num), dtype=np.float32)
u2 = np.array([-2, -2])
o2 = 3*np.array([[1, 0],
[0, 1]])
a2 = (pos-u2).dot(np.linalg.inv(o2))
b2 = np.expand_dims(pos-u2,axis=3)
Z2 = np.zeros((num,num), dtype=np.float32)
for i in range(num):
Z1[i] = [np.dot(a1[i,j],b1[i,j]) for j in range(num)]
Z2[i] = [np.dot(a2[i,j],b2[i,j]) for j in range(num)]
Z1 = np.exp(Z1*(-0.5))/(2*np.pi*np.linalg.det(o1))
Z2 = np.exp(Z2*(-0.5))/(2*np.pi*np.linalg.det(o1))
Z = Z1 + Z2
fig = plt.figure()
ax = fig.add_subplot(211,projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, alpha=0.3, cmap=cm.coolwarm)
cset = ax.contour(X,Y,Z,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-5,cmap=mpl.cm.winter)
cset = ax.contour(X, Y, Z, zdir='y', offset= 5,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr # 蓝,白,红
cm.coolwarm
'''
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
ax2 = fig.add_subplot(212)
cs = ax2.contour(X,Y,Z)
ax2.clabel(cs, inline=1, fontsize=20)
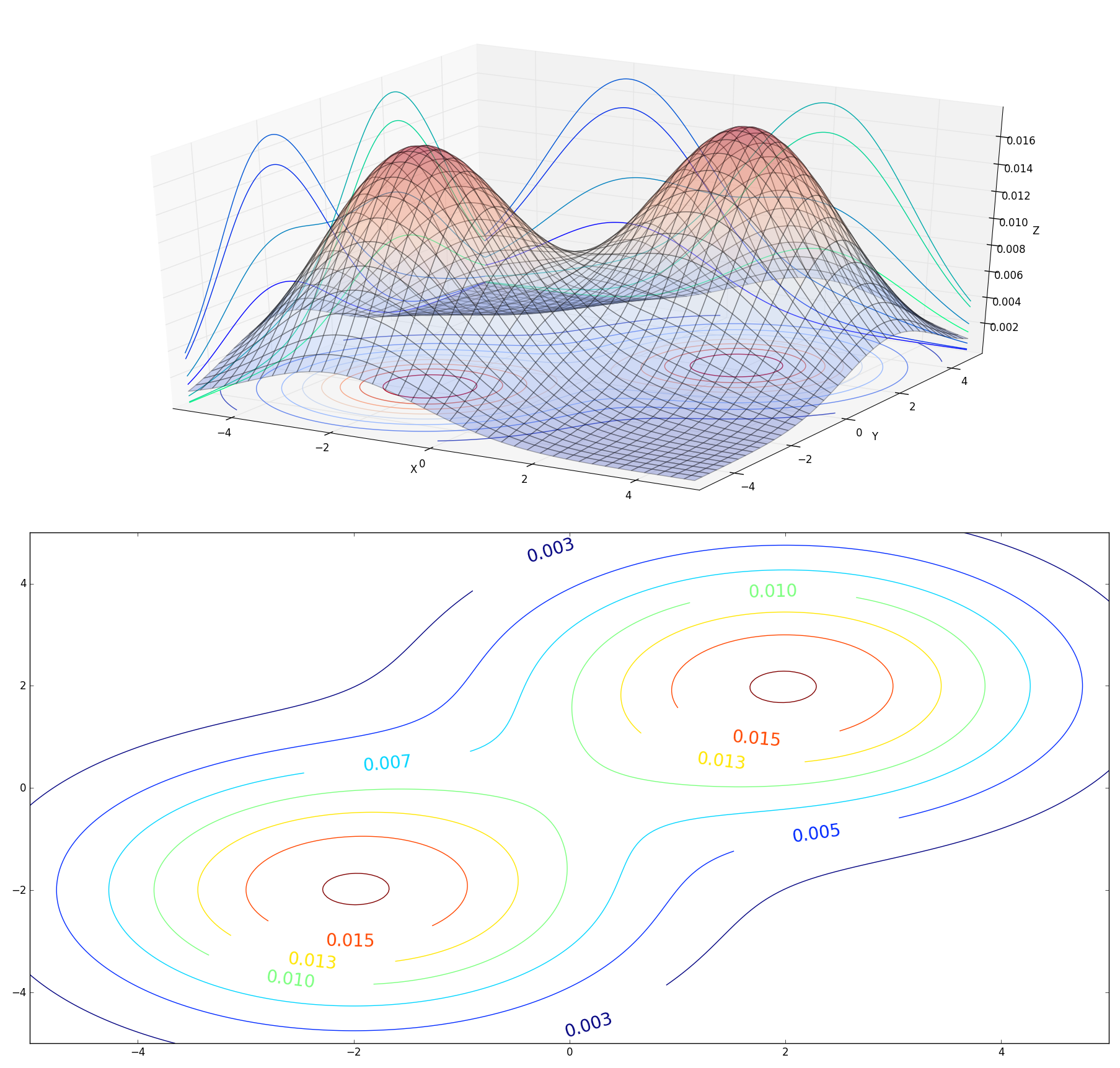
不过吴老大的图两个高斯分布投影是分开的,所以我们再次小改绘图部分,
cset = ax.contour(X,Y,Z1,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X,Y,Z2,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-5,cmap=mpl.cm.winter)
cset = ax.contour(X, Y, Z, zdir='y', offset= 5,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr # 蓝,白,红
cm.coolwarm
'''
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
ax2 = fig.add_subplot(212)
cs = ax2.contour(X,Y,Z1)
ax2.clabel(cs, inline=1, fontsize=20)
cs2 = ax2.contour(X,Y,Z2)
ax2.clabel(cs2, inline=1, fontsize=20)
显示如下,框子不够标准导致圆有点变形,不过这个可以通过手动拉伸得到优化,所以问题不大,

有关多元正态分布的数学原理建议自行百度(cs229的学习不会在博客上更新,主要是因为我非常非常讨厌打数学公式233)。