【原题】
Description
Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.
Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.
There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.
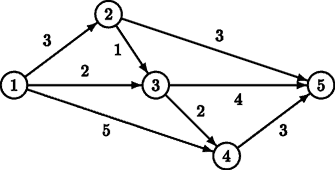
For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.
Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.
Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
-
One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
-
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
-
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.
Output
For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 109 = 1,000,000,000.
Sample
Input
2 5 8 1 2 3 1 3 2 1 4 5 2 3 1 2 5 3 3 4 2 3 5 4 4 5 3 1 5 5 6 2 3 1 3 2 1 3 1 10 4 5 2 5 2 7 5 2 7 4 1
Output
3 2
Hint
The first test case above corresponds to the picture in the problem description.
【思路】记录最短路和次短路,用其进行松弛。
1 #include <algorithm> 2 #include <cmath> 3 #include <cstdio> 4 #include <cstring> 5 #include <list> 6 #include <map> 7 #include <iostream> 8 #include <queue> 9 #include <set> 10 #include <stack> 11 #include <string> 12 #include <vector> 13 #include <iomanip> 14 #define LL long long 15 #define inf 0x3f3f3f3f 16 #define INF 0x3f3f3f3f3f3f 17 #define PI 3.1415926535898 18 #define F first 19 #define S second 20 #define lson rt << 1 21 #define rson rt << 1 | 1 22 using namespace std; 23 24 const int maxn = 1e3 + 7; 25 const int maxm = 1e4 + 7; 26 int vis[maxn][2], num[maxn][2]; 27 int dis[maxn][2]; 28 int n, m; 29 30 struct pp 31 { 32 int v, next, w; 33 }edge[maxm]; 34 int head[maxn]; 35 int cnt = 0; 36 struct node 37 { 38 int u, flag, dis; 39 bool operator < (const node& a) const 40 { 41 return a.dis < dis; 42 } 43 }; 44 void add(int t1, int t2, int t3) 45 { 46 edge[++cnt].v = t2; 47 edge[cnt].w = t3; 48 edge[cnt].next = head[t1]; 49 head[t1] = cnt; 50 } 51 int dijkstra(int b, int end) 52 { 53 priority_queue<node> que; 54 int i; 55 for (int i = 1; i <= n; i++) 56 { 57 vis[i][0] = vis[i][1] = 0; 58 dis[i][0] = dis[i][1] = inf; 59 num[i][0] = num[i][1] = 0; 60 } 61 dis[b][0] = 0; 62 num[b][0] = 1; 63 node temp; 64 temp.u = b, temp.dis = 0, temp.flag = 0; 65 que.push(temp); 66 while (!que.empty()) 67 { 68 int u = que.top().u; 69 int sta = que.top().flag; 70 que.pop(); 71 if (vis[u][sta]) continue; 72 vis[u][sta] = 1; 73 for (i = head[u]; i; i = edge[i].next) 74 { 75 int v = edge[i].v; 76 int dst = dis[u][sta] + edge[i].w; 77 if (dis[v][0] > dst) 78 { 79 if (dis[v][0] != inf) 80 { 81 dis[v][1] = dis[v][0]; 82 num[v][1] = num[v][0]; 83 temp.u = v, temp.dis = dis[v][1], temp.flag = 1; 84 que.push(temp); 85 } 86 dis[v][0] = dst; 87 num[v][0] = num[u][sta]; 88 temp.u = v, temp.dis = dis[v][0], temp.flag = 0; 89 que.push(temp); 90 } 91 else if (dis[v][0] == dst) 92 { 93 num[v][0] += num[u][sta]; 94 } 95 else if (dis[v][1] > dst) 96 { 97 dis[v][1] = dst; 98 num[v][1] = num[u][sta]; 99 temp.u = v, temp.dis = dis[v][1], temp.flag = 1; 100 que.push(temp); 101 } 102 else if (dis[v][1] == dis[u][sta] + edge[i].w) 103 { 104 num[v][1]+= num[u][sta]; 105 } 106 } 107 } 108 if (dis[end][0] - dis[end][1] == -1) return num[end][0] + num[end][1]; 109 return num[end][0]; 110 } 111 112 int main() 113 { 114 ios::sync_with_stdio(false); 115 cin.tie(0); 116 int t; 117 scanf("%d", &t); 118 while (t--) 119 { 120 memset(head, 0, sizeof(head)); 121 scanf("%d%d", &n, &m); 122 cnt = 0; 123 int ta, tb, tv; 124 for (int i = 1; i <= m; i++) 125 { 126 scanf("%d%d%d", &ta, &tb, &tv); 127 add(ta, tb, tv); 128 } 129 int s, f; 130 scanf("%d%d", &s, &f); 131 int res = dijkstra(s, f); 132 printf("%d ", res); 133 } 134 }