剑指offer 26. 二叉搜索树与双向链表 & leetcode 剑指 Offer 36. 二叉搜索树与双向链表

 26. 二叉搜索树与双向链表 & 剑指 Offer 36. 二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

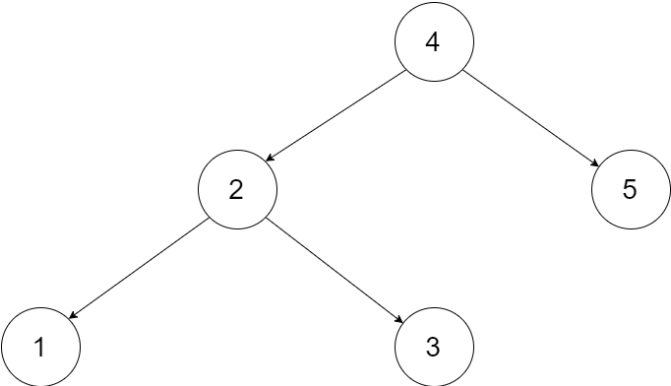
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

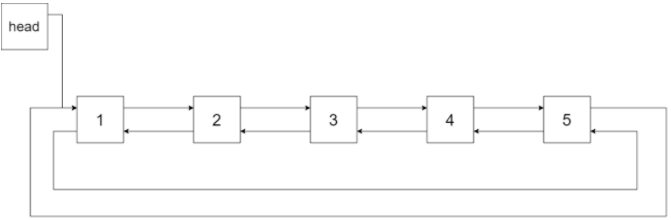
 特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

思路一：

1. 非递归中序遍历二叉树

2. 两个指针，一个指向前一个结点，一个指向当前结点，

3. 前一个指针的右指针指向当前结点，当前结点的左指针指向前一个节点（不要漏了这行，因为不是所有的left指针都指向上个结点， 比如上面的4和3， 就需要手动将4结点的left指针指向3），

4. pre后移

5. 头尾相接

class Solution {

    public Node treeToDoublyList(Node root) {
        // 非递归中序遍历
        if(root == null){
            return root;
        }
        Stack<Node> stack = new Stack<>();
        Node head = null, pre = null, cur = root;
        while(!stack.isEmpty() || cur != null){
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            if(pre == null){
                head = cur;
            }else{
                pre.right = cur;
                cur.left = pre;     // 不要漏了这行，因为不是所有的left指针都指向上个结点
            }
            pre = cur;
            cur = cur.right;
        }
        // 首尾相接
        head.left = pre;
        pre.right = head;
        return head;
    }
}

leetcode 运行时间为1 ms > 19.39%, 空间为38.2 MB > 88.58%

复杂度分析：

时间复杂度：使用非递归中序遍历遍历了整棵树，所以时间复杂度为O(n)

空间复杂度：需要一个栈，栈的大小最大为树的高度，树高最大为O(n), 最小为O(logn), 所以空间复杂度最好为O(logn), 最差为O(n)

思路二：递归非中序遍历

思路参考：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/solution/mian-shi-ti-36-er-cha-sou-suo-shu-yu-shuang-xian-5/

把 head、pre 指针定义成全局变量，可以省去如何递归之间传递指针的思考

class Solution {

    Node head = null, pre = null;

    public Node treeToDoublyList(Node root) {
        // 递归中序遍历
        if(root == null){
            return null;
        }
        midOrder(root);
        // 首尾相接
        head.left = pre;
        pre.right = head;
        return head;
    }

    public void midOrder(Node root){
        if(root == null){
            return ;
        }
        midOrder(root.left);
        if(head == null){
            head = root;
        }else{
            pre.right = root;
        }
        root.left = pre;
        pre = root;
        midOrder(root.right);
    }
}

leetcode 运行时间为0 ms > 100.00%, 空间为38.4 MB > 56.50%

复杂度分析：

时间复杂度：使用递归中序遍历遍历了整棵树，所以时间复杂度为O(n)

空间复杂度：需要一个递归栈，栈的大小最大为树的高度，树高最大为O(n), 最小为O(logn), 所以空间复杂度最好为O(logn), 最差为O(n)

思路三：

1. 中序递归遍历二叉树， 把所有结点都存下来

2. 把数组中的结点链接成一个双向链表

class Solution {

    public Node treeToDoublyList(Node root) {
        // 使用递归中序遍历把结点都存在一个集合中，然后遍历集合，修改每个结点的指向
        if(root == null){
            return null;
        }

        ArrayList<Node> list = new ArrayList<>();

        midOrder(root, list);
        for(int i = 0;  i < list.size() - 1; i++){
            list.get(i).right = list.get(i+1);
            list.get(i+1).left = list.get(i);
        }
        // 首尾相接
        list.get(0).left = list.get(list.size()-1);
        list.get(list.size()-1).right = list.get(0);
        return list.get(0);
    }

    public void midOrder(Node root, ArrayList<Node> list){
        if(root == null){
            return ;
        }
        midOrder(root.left, list);
        list.add(root);
        midOrder(root.right, list);
    }
}

leetcode 运行时间为1 ms > 19.39%, 空间为38.7 MB > 16.49%

复杂度分析：

时间复杂度：首先使用递归中序遍历遍历了整棵树，花费的时间为O(n)，随后遍历存储了所有结点的集合，花费的时间也为O(n), 所以整体时间复杂度为O(2n)

空间复杂度：首先递归遍历需要一个递归栈，栈的大小最大为树的高度，树高最大为O(n), 最小为O(logn), 所以花费的空间最少为为O(logn), 最多为O(n)；其次需要一个集合存储所有结点，需要O(n)的空间，所以整体的空间复杂度为O(2n)