目录
这篇使用动态规划算法来解决这个问题,借这篇博客初窥动态规划算法。最少钱币数问题也可以看作多重背包问题。
那么什么是动态规划算法?
动态规划(dynamic programming,DP)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。1957年出版了他的名著《Dynamic Programming》,这是该领域的第一本著作。(思想也有点像分布式处理)
———From Baidupedia
那么我们如何去描述它?
动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度, 因此它比回溯法、暴力法等要快许多。
——From 从动态规划新手到专家
概念讲完,开始做题。
题目:
| 问题描述 | 这是一个古老而又经典的问题。用给定的几种钱币凑成某个钱数,一般而言有多种方式。例如:给定了 6 种钱币面值为 2、5、10、20、50、100,用来凑 15 元,可以用 5 个 2 元、1个 5 元,或者 3 个 5 元,或者 1 个 5 元、1个 10 元,等等。显然,最少需要 2 个钱币才能凑成 15 元。 你的任务就是,给定若干个互不相同的钱币面值,编程计算,最少需要多少个钱币才能凑成某个给出的钱数。 |
| 输入形式 | 输入可以有多个测试用例。每个测试用例的第一行是待凑的钱数值 M(1 <= M<= 2000,整数),接着的一行中,第一个整数 K(1 <= K <= 10)表示币种个数,随后是 K个互不相同的钱币面值 Ki(1 <= Ki <= 1000)。输入 M=0 时结束。 |
| 输出形式 | 每个测试用例输出一行,即凑成钱数值 M 最少需要的钱币个数。如果凑钱失败,输出“Impossible”。你可以假设,每种待凑钱币的数量是无限多的。 |
| 样例输入 | 15 6 2 5 10 20 50 100 1 1 2 0 |
| 样例输出 | 2 Impossible |
分析:
上一篇最少钱币数-1-贪心算法(错,或者叫有问题)-CCF-CSP练习题中使用的贪心算法解决的凑硬币问题,有些情况下是可以得出正解的,比如后一个钱币面值没有达到前一个钱币面值的2倍时;但对于某些情况来说得出的解是错误的。比如有3种面值分别为3元,5元,7元的纸币,(1)那么至少用几张纸币能凑够10元?我的直觉告诉我先选面值最大的,7元一张,然后再选面值5元的时候发现超额了(7+5>10),因此我们选3元一张,最少用2张纸币就能凑够10元,这个时候可以得出正解。这个方法容易想出来,抽象一点可以叫贪心算法(每次都选当前看来最好的选择,不从整体最优考虑),(2)那么至少用几张纸币能凑够8元呢?如果还按照贪心算法来解的话会得到Impossible。因为先选一张7元,然后再选5元(7+5>8)不行,换选3元(7+3>8)还不行。但是仔细看会发现5元+3元不是8元吗,怎么会无解。所以贪心算法解这个问题是不行的。考CSP时只能用来骗点分。
到这里我们发现用贪心算法会出现两个问题 1)本来有解用贪心法算出来却无解,例如上例(2)至少用几张纸币能凑够8元?;2)算出来的解不是最优解,例如有 1元,7元,9元,10元四种面值的纸币,要凑18元 ,贪心算法会给出答案需要3张(10元1张,7元1张,1元1张),但是我们可以明显看出 2张(两张9元)也可以。
那么问题出在了哪里?在这里用贪心算法是有条件的——后一个的权值(这里就是纸币面值)是前一个的2倍或以上才可以使用,这里10不到9的两倍。贪心算法不是对所有问题都能得到整体最优解。关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。在这里我们先选择了10元,在第二步的时候9元就选择不了了(10+9>18了),所以会错过9+9这个最优解。所以说贪心算法在对问题求解时,总是做出在当前看来是最好的选择,不从整体最优考虑。
这里说了这么多,都是在讨论上一篇,本篇主要讨论正确解法——动态规划算法解题。可能你已经不耐烦了,那么先上一个此问题递推公式(也可以叫做动态转移方程):(注:v[i]表示可以使用的纸币的面额组成的数组,dp[m]表示要凑m元至少需要多少张纸币。)
dp[m] = min(dp[m-v[i] ]+1,dp[m])那么这个方程怎么得来的呢?我们先了解一下DP(Dynamic Programing)的基本原理:首先,找到某个状态的最优解,然后在它的帮助下,找到下一个状态的最优解。不明白这个概念没关系,我们以上面的例子为例来分析一下——如果我们有4种面值分别为1元,3元,5元,7元的纸币,那么至少需要几张纸币就能凑出8元?
在分析这个问题之前先来思考一个问题,至少用多少张纸币能凑够m(表示money)元(m<8)呢?为什么要这么问呢? 动态规划的思想:(1)当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。 (2)这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。
让我们从规模最小的m开始。当m=0时,即我们需要多少个币来凑够0元呢? 由于1,3,5,7都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个币。 (em......Interesting,这个分析很傻是不是?别着急,这个思路有利于我们理清动态规划究竟在做些什么。) 为了方便我们用dp[m]=c来表示凑够m元最少需要c个硬币。于是我们就得到了dp[0]=0, 表示凑够0元最小需要0个硬币。当m=1时,只有面值为1元的硬币可用, 因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道的dp[0]=0。所以,dp[1]=dp[1-1]+1=dp[0]+1=0+1=1。当m=2时, 仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币, 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量),而这个答案也已经知道了。 所以dp[2]=dp[2-1]+1=dp[1]+1=1+1=2。分析到这里,聪明的你可能已经看出端倪,没看出来没关系,接下来让我们看看m=3时的情况。当m=3时我们能用的硬币就有两种了:1元的和3元的( 5元的仍然没用,因为你需要凑的数目是3元,5元面值太大了)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个1元的硬币,我的目标就变为了: 凑够3-1=2元需要的最少硬币数量。即dp[3]=dp[3-1]+1=dp[2]+1=2+1=3。 这个方案说的是,我拿3个1元的硬币;第二种方案是我拿起一个3元的硬币, 我的目标就变成:凑够3-3=0元需要的最少张纸币。即dp[3]=dp[3-3]+1=dp[0]+1=0+1=1. 这个方案说的是,我拿1个3元的硬币。好了,这两种方案哪种更优呢? 记得我们的问题是要用最少的硬币数量来凑够3元。所以, 选择dp[3]=1,怎么来的呢?具体是这样得到的:dp[3]=min(dp[3-1]+1, dp[3-3]+1)。
有了上面的分析,这回应该能看出个门道了吧,你可能早已按奈不住了,现在我们就可以从以上分析抽象出我们想要的东西了——递推公式。从以上的文字中, 我们要抽出动态规划里非常重要的两个概念:状态和状态转移方程。
上文中dp[m]表示凑够m元需要的最少硬币数量,我们将它定义为该问题的"状态", 这个状态是怎么找出来的呢?是根据子问题定义状态。你找到子问题,状态也就浮出水面了。 最终我们要求解的问题,可以用这个状态来表示:dp[8],即凑够8元最少需要多少个硬币。 那状态转移方程是什么呢?既然我们用dp[m]表示状态,那么状态转移方程自然包含dp[m], 上文中包含状态 dp[m] 的方程是:dp[3]=min(dp[3-1]+1, dp[3-3]+1)。没错, 它就是状态转移方程,描述状态之间是如何转移的。当然,我们要对它抽象一下,dp[m] = min(dp[ m-v[i] ]+1,dp[m]),其中 m-v[i] >=0,v[i] 表示第i个硬币的面值,方程的含义是拿出一个面值为 v[i] 的硬币后,凑够 m-v[i] 元至少需要的硬币数目(dp[m-v[i] ])+1和凑够m元至少需要的硬币数目(dp[m])相比较,取较小的存入dp[m]。
这里可能就会有人问了,为什么还要和dp[m]比较后再存入dp[m],正如上面的例子,因为我们在凑够m元时,可能有多种可行的方案,我们要比较出哪一种方案所需硬币数目最小。例如在4种硬币1、3、5、7元凑8元的时候会有三种方案,1)8个1元;2)3+5元;3)1+7元。我们得从中找到我们所要的答案。(如果用贪心算法的话可能会错过最优解)
有了动态转移方程,问题基本就算解决了。当然,Talk is cheap,show me the code!
C++动态转移方程代码:
#include <iostream>
using namespace std;
int main()
{
int coins[10] = {0}; //硬币面值数组,由于题目给出不超过10种,所以我申请了10。
int money = 0; //待凑钱的数值*/
int kind = 0; //钱币种类数目*/
while(1)
{
cin >> money;
if(0 == money)break; //结束标志
int dp[money+1]; //动态规划数组
dp[0] = 0; //初始化第一个元素为0,因为要凑0元需要0个钱币
cin >> kind; //硬币面值种类数
for(int k=0; k<kind; k++)
{
cin >> coins[k]; //读入硬币面值,存入数组coins[]
}
for(int i = 1; i <= money; i++) dp[i] = 99999; //初始化数组dp[],设置dp[i]等于无穷大
for(int i = 1; i <= money; i++) //从凑1元开始,一直算到money元为止。
{
for(int j = 0; j < kind; j++)
{
if(i >= coins[j])
{
dp[i] = min(dp[i- coins[j] ] + 1, dp[i]);
}
/*****也可以写成******
if(i >= coins[j] && dp[i - coins[j]] + 1 < dp[i])
{
dp[i] = dp[i- coins[j] ] + 1;
}
自己干了,不用麻烦min()函数
*/
}
}
if( dp[money] == 99999 )
{
cout << "Impossible"<< endl;
}
else
{
cout << dp[money] << endl;
}
}
return 0;
}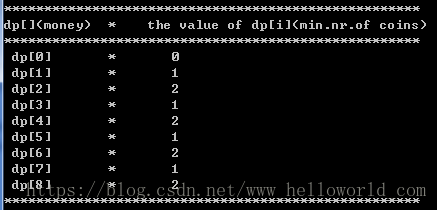
如图1-1所示,有4种面值的钱币1元、3元、5元、7元时,从凑0元到凑8元至少所需钱币数。
总结:
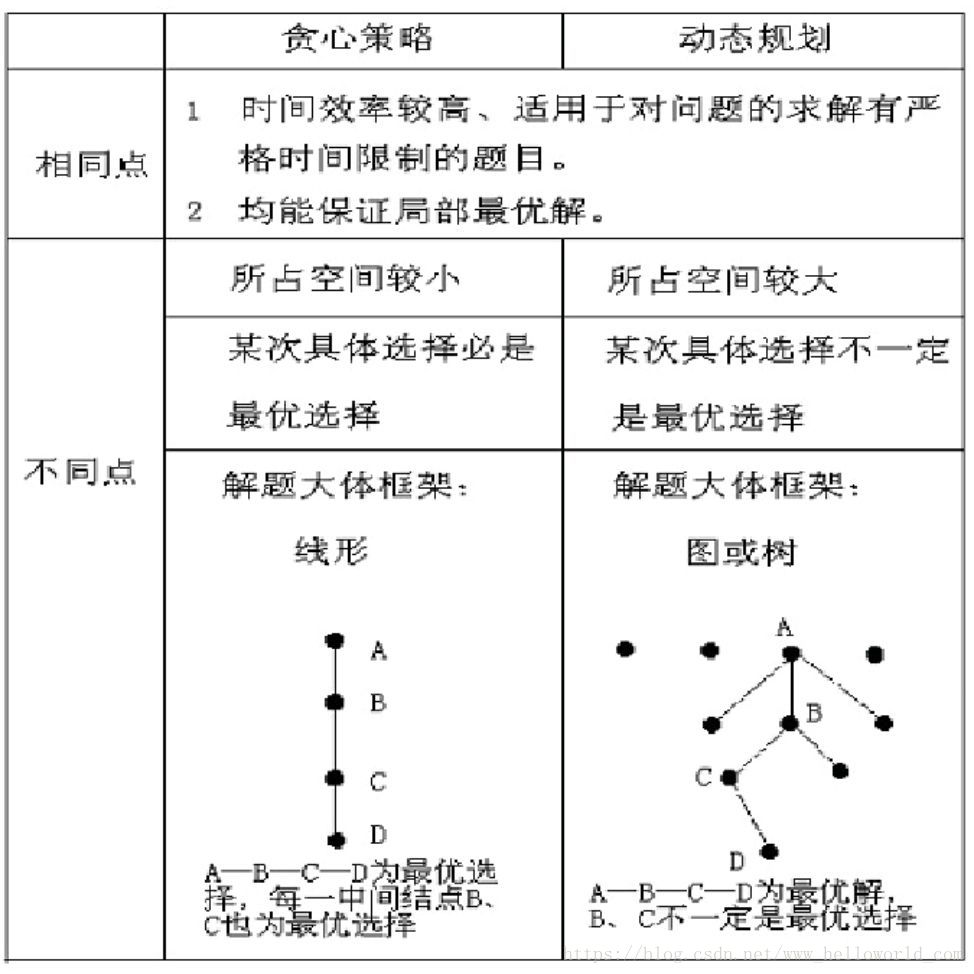
使用动态规划算法解决此题时,能全面的考虑到所有情况,从而找到最优解。但是相对于贪心算法来说时间和空间复杂度都会增加。这两个算法有什么区别呢?如图1-2所示。
动态规划算法不是一个具体的算法,动态规划算法要求我们具体问题具体分析。把一个大的问题变为一个和它同质的(除了规模变小,其他都一样)小规模问题。然后推导出递推公式(状态转移方程)。这是关键。那么这个推导递推公式的能力怎么获得呢?
动态规划程序设计是对解最优化问题的一种途径、一种方法,而不是一种特殊算法。不像搜索或数值计算那样,具有一个标准的数学表达式和明确清晰的解题方法。动态规划程序设计往往是针对一种最优化问题,由于各种问题的性质不同,确定最优解的条件也互不相同,因而动态规划的设计方法对不同的问题,有各具特色的解题方法,而不存在一种万能的动态规划算法,可以解决各类最优化问题。因此读者在学习时,除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论,逐渐学会并掌握这一设计方法。 ——From Baidupedia
最后一点总结,写完东西一定要保存,刚刚去吃饭忘记保存,结果重新写了俩多小时。
参考博文:从动态规划新手到专家