TreeMap

红黑树又称红-黑二叉树，它首先是一颗二叉树，它具体二叉树所有的特性。同时红黑树更是一颗自平衡的排序二叉树。

我们知道一颗基本的二叉树他们都需要满足一个基本性质--即树中的任何节点的值大于它的左子节点，且小于它的右子节点。按照这个基本性质使得树的检索效率大大提高。我们知道在生成二叉树的过程是非常容易失衡的，最坏的情况就是一边倒（只有右/左子树），这样势必会导致二叉树的检索效率大大降低（O(n)），所以为了维持二叉树的平衡，大牛们提出了各种实现的算法，如：AVL，SBT，伸展树，TREAP ，红黑树等等。

平衡二叉树必须具备如下特性：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。也就是说该二叉树的任何一个等等子节点，其左右子树的高度都相近。

红黑树顾名思义就是节点是红色或者黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。对于一棵有效的红黑树二叉树而言我们必须增加如下规则：

红黑树（RBT）的定义：它或者是一颗空树，或者是具有一下性质的二叉查找树：
1.节点非红即黑。
2.根节点是黑色。
3.所有NULL结点称为叶子节点，且认为颜色为黑。
4.所有红节点的子节点都为黑色。
5.从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

简单说说：
第3条，显然这里的叶子节点不是平常我们所说的叶子节点，如图标有NIL的为叶子节点，为什么不按常规出牌，因为按一般的叶子节点也行，但会使算法更复杂；
第4条，即该树上决不允许存在两个连续的红节点；
第5条，比如图中红8到1左边的叶子节点的路径包含2个黑节点，到6下的叶子节点的路径也包含2个黑节点。
所有性质1-5合起来约束了该树的平衡性能--即该树上的最长路径不可能会大于2倍最短路径。
为什么？因为第1条该树上的节点非红即黑，由于第4条该树上不允许存在两个连续的红节点，那么对于从一个节点到其叶子节点的一条最长的路径一定是红黑交错的，那么最短路径一定是纯黑色的节点；
而又第5条从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点，这么来说最长路径上的黑节点的数目和最短路径上的黑节点的数目相等！而又第2条根结点为黑、第3条叶子节点是黑，那么可知：最长路径<=2*最短路径。
一颗二叉树的平衡性能越好，那么它的效率越高！显然红黑树的平衡性能比AVL的略差些，
但是经过大量试验证明，实际上红黑树的效率还是很不错了，仍能达到O(logN)，至少知道他的时间复杂度一定小于2O(logN)!

TreeMap：

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable
{
    /**
     * The comparator used to maintain order in this tree map, or
     * null if it uses the natural ordering of its keys.
     *
     * @serial
     */
    private final Comparator<? super K> comparator;

    private transient Entry<K,V> root;

    /**
     * The number of entries in the tree
     */
    private transient int size = 0;

    /**
     * The number of structural modifications to the tree.
     */
    private transient int modCount = 0;

上面是treemap一部分源码

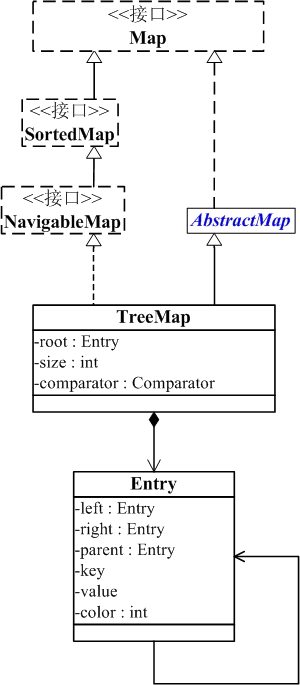
(01) TreeMap实现继承于AbstractMap，并且实现了NavigableMap接口。
(02) TreeMap的本质是R-B Tree(红黑树)，它包含几个重要的成员变量： root, size, comparator。

root 是红黑数的根节点。它是Entry类型，Entry是红黑数的节点，它包含了红黑数的6个基本组成成分：key(键)、value(值)、left(左孩子)、right(右孩子)、parent(父节点)、color(颜色)。Entry节点根据key进行排序，Entry节点包含的内容为value。
红黑数排序时，根据Entry中的key进行排序；Entry中的key比较大小是根据比较器comparator来进行判断的。
size是红黑数中节点的个数。

使用：

key-value遍历：

// 假设map是TreeMap对象  
// map中的key是String类型，value是Integer类型  
Integer integ = null;  
Iterator iter = map.entrySet().iterator();  
while(iter.hasNext()) {  
    Map.Entry entry = (Map.Entry)iter.next();  
    // 获取key  
    key = (String)entry.getKey();  
        // 获取value  
    integ = (Integer)entry.getValue();  
}  

key遍历：

// 假设map是TreeMap对象  
// map中的key是String类型，value是Integer类型  
String key = null;  
Integer integ = null;  
Iterator iter = map.keySet().iterator();  
while (iter.hasNext()) {  
        // 获取key  
    key = (String)iter.next();  
        // 根据key，获取value  
    integ = (Integer)map.get(key);  
}  

values遍历：

// 假设map是TreeMap对象  
// map中的key是String类型，value是Integer类型  
Integer value = null;  
Collection c = map.values();  
Iterator iter= c.iterator();  
while (iter.hasNext()) {  
    value = (Integer)iter.next();  
}  

对于红黑二叉树而言它主要包括三大基本操作：左旋、右旋、着色。

http://blog.csdn.net/x_i_y_u_e/article/details/46372023

http://www.cnblogs.com/chenssy/p/3746600.html

https://zhuanlan.zhihu.com/p/24795143

http://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw==&mid=2653191832&idx=1&sn=12017161025495c6914b5ab9397baa59&chksm=8c990c42bbee8554ba02eb83d839123bd3bead6ffc736111456ea77367a3df75750cf88016e0&scene=21#wechat_redirect

https://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html

https://www.cnblogs.com/skywang12345/p/3245399.html