Paxos:
Paxos算法背景介绍:
Paxos算法是分布式技术大师Lamport提出的,主要目的是通过这个算法,让参与分布式处理的每个参与者逐步达成一致意见。用好理解的方式来说,就是在一个选举过程中,让不同的选民最终做出一致的决定。
Lamport为了讲述这个算法,假想了一个叫做Paxos的希腊城邦进行选举的情景,这个算法也是因此而得名。
在他的假想中,这个城邦要采用民主提议和投票的方式选出一个最终的决议,但由于城邦的居民没有人愿意把全部时间和精力放在这种事情上,所以他们只能不定时的来参加提议,不定时来了解提议、投票进展,不定时的表达自己的投票意见。
Paxos算法的目标就是让他们按照少数服从多数的方式,最终达成一致意见。
Paxos算法的具体情况:
1、在整个提议和投票过程中,主要的角色就是“提议者”(向“接受者”提出提议)和“接受者”(收到“提议者”的提议后,向“提议者”表达自己的意见)。
2、整个算法的大致过程为:
第一阶段:因为存在多个“提议者”,如果都提意见,那么“接受者”接受谁的不接受谁的?太混乱了。所以,要先明确哪个“提议者”是意见领袖有权提出提议,未来,“接受者”们就主要处理这个“提议者”的提议了(这样,也可以在提出提议时就尽量让意见统一,谋求尽早形成多数派)。
第二阶段:由上阶段选出的意见领袖提出提议,“接受者”反馈意见。如果多数“接受者”接受了一个提议,那么提议就通过了。
必须要了解的其他相关背景:
1)怎么明确意见领袖呢?通过编号。每个“提议者”在第一阶段先报个号,谁的号大,谁就是意见领袖。如果不好理解,可以想象为贿选。每个提议者先拿着钞票贿赂一圈“接受者”,谁给的钱多,第二阶段“接受者”就听谁的。(注:这里和下文提到的“意见领袖”,并不是一个新的角色,而是代表在那一轮贿赂成功的“提议者”。所以,请把意见领袖理解为贿赂中胜出的“提议者”即可)
2)有个跟选举常识不一样的地方,就是每个“提议者”不会执着于让自己的提议通过,而是每个“提议者”会执着于让提议尽快达成一致意见。所以,为了这个目标,如果“提议者”在贿选的时候,发现“接受者”已经接受过前面意见领袖的提议了,即便“提议者”贿选成功,也会默默的把自己的提议改为前面意见领袖的提议。所以一旦贿赂成功,胜出的“提议者”再提出提议,提议内容也是前面意见领袖的提议(这样,在谋求尽早形成多数派的路上,又前进了一步)。
3)钱的多少很重要,如果钱少了,无论在第一还是第二阶段“接受者”都不会尿你,直接拒绝。
4)上面2)中讲到,如果“提议者”在贿选时,发现前面已经有意见领袖的提议,那就将自己的提议默默改成前面意见领袖的提议。这里有一种情况,如果你是“提议者”,在贿赂的时候,“接受者1”跟你说“他见过的意见领袖的提议是方案1”,而“接受者2”跟你说“他见过的意见领袖提议是方案2”,你该怎么办?这时的原则也很简单,还是:钱的多少很重要!你判断一下是“接受者1”见过的意见领袖有钱,还是“接受者2”见过的意见领袖有钱?如何判断呢?因为“接受者”在被“提议者”贿赂的时候,自己会记下贿赂的金额。所以当你贿赂“接受者”时,一旦你给的贿赂多而胜出,“接受者”会告诉你两件事情:a.前任意见领袖的提议内容(如果有的话),b.前任意见领袖当时贿赂了多少钱。这样,再面对刚才的情景时,你只需要判断一下“接受者1”和“接受者2”告诉你的信息中,哪个意见领袖当时给的钱多,那你就默默的把自己的提议,改成那个意见领袖的提议。
5)最后这一部分最有意思,但描述起来有点绕,如果不能一下子就理解可以先看后面的例子。在整个选举过程中,每个人谁先来谁后到,“接受者”什么时间能够接到“提议者”的信息,是完全不可控的。所以很可能一个意见领袖已经产生了,但是由于这个意见领袖的第二阶段刚刚开始,绝大部分“接受者”还没有收到这个意见领袖的提议。结果,这时突然冲进来了一个新的土豪“提议者”,那么这个土豪“提议者”也是有机会让自己的提议胜出的!这时就形成了一种博弈:a.上一个意见领袖要赶在土豪“提议者”贿赂到“接受者”前,赶到“接受者”面前让他接受自己的提议,否则会因为自己的之前贿赂的钱比土豪少而被拒绝。b.土豪“提议者”要赶在上一个意见领袖将提议传达给“接受者”前,贿赂到“接受者”,否则土豪“提议者”即便贿赂成功,也要默默的将自己的提议改为前任意见领袖的提议。这整个博弈的过程,最终就看这两个“提议者”谁的进展快了。但最终一定会有一个意见领袖,先得到多数“接受者”的认可,那他的提议就胜出了。
总结:
好啦,故事到这里基本讲述完了,咱们来总结一下,其实Paxos算法就下面这么几个原则:
1)Paxos算法包括两个阶段:第一个阶段主要是贿选,还没有提出提议;第二个阶段主要根据第一阶段的结果,明确接受谁的提议,并明确提议的内容是什么(这个提议可能是贿选胜出“提议者”自己的提议,也可能是前任意见领袖的提议,具体是哪个提议,见下面第3点原则)。
2)编号(贿赂金额)很重要,无论在哪个阶段,编号(贿赂金额)小的,都会被鄙视(被拒绝)。
3)在第一阶段中,一旦“接受者”已经接受了之前意见领袖的提议,那后面再来找这个“接受者”的“提议者”,即便在贿赂中胜出,也要被洗脑,默默将自己的提议改为前任意见领袖的提议,然后他会在第二阶段提出该提议(也就是之前意见领袖的提议,以力争让大家的意见趋同)。如果“接受者”之前没有接受过任何提议,那贿选胜出的“提议者”就可以提出自己的提议了。
举例:
最后举个例子,加深一下印象:
有两个“提议者”和三个“接受者”。
1)首先“提议者1”贿赂了3个“接受者”
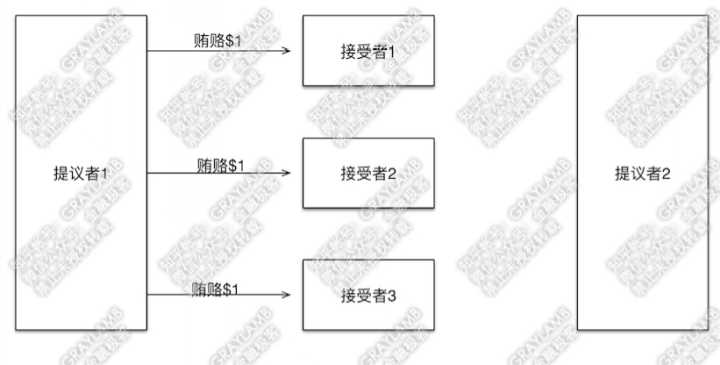
2)3个“接受者”记录下贿赂金额,因为目前只有一个“提议者”出价,因此$1就是最高的了,所以“接受者”们返回贿赂成功。
此外,因为没有任何先前的意见领袖提出的提议,因此“接受者”们告诉“提议者1”没有之前接受过的提议(自然也就没有上一个意见领袖的贿赂金额了)。

3)“提议者1”向“接受者1”提出了自己的提议:1号提议,并告知自己之前已贿赂$1。
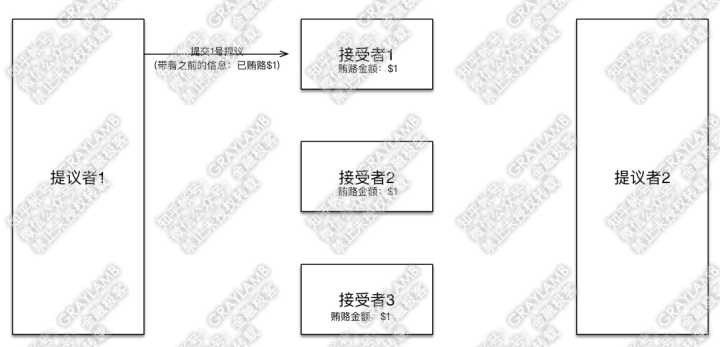
4)“接受者1”检查了一下,目前记录的贿赂金额就是$1,于是接受了这一提议,并把1号提议记录在案。

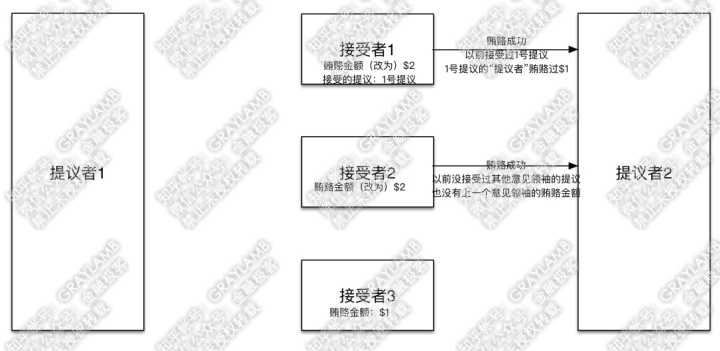
5)在“提议者1”向“接受者2”“接受者3”发起提议前,土豪“提议者2”出现,他开始用$2贿赂“接受者1”与“接受者2”。

6)“接受者1”与“接受者2”立刻被收买,将贿赂金额改为$2。但是,不同的是:“接受者1”告诉“提议者2”,之前我已经接受过1号提议了,同时1号提议的“提议者”贿赂过$1;而,“接受者2”告诉“提议者2”,之前没有接受过其他意见领袖的提议,也没有上一个意见领袖的贿赂金额。
7)这时,“提议者1”回过神来了,他向“接受者2”和“接受者3”发起1号提议,并带着信息“我前期已经贿赂过$1”。
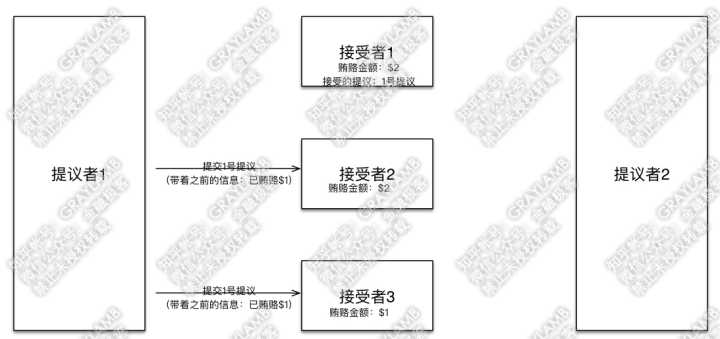
8)“接受者2”“接受者3”开始答复:“接受者2”检查了一下自己记录的贿赂金额,然后表示,已经有人出价到$2了,而你之前只出到$1,不接受你的提议,再见。
但“接受者3”检查了一下自己记录的贿赂金额,目前记录的贿赂金额就是$1,于是接受了这一提议,并把1号提议记录在案。
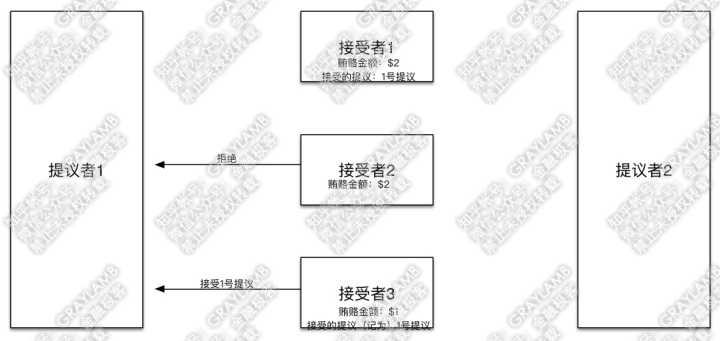
9)到这里,“提议者1”已经得到两个接受者的赞同,已经得到了多数“接受者”的赞同。于是“提议者1”确定1号提议最终通过。
10)下面,回到“提议者2”。刚才说到,“提议者2”贿赂了“接受者1”和“接受者2”,被“接受者1”告知:“之前已经接受过1号提议了,同时1号提议的‘提议者’贿赂过$1”,并被“接受者2”告知:“之前没有接到过其他意见领袖的提议,也没有其他意见领袖的贿赂金额”。
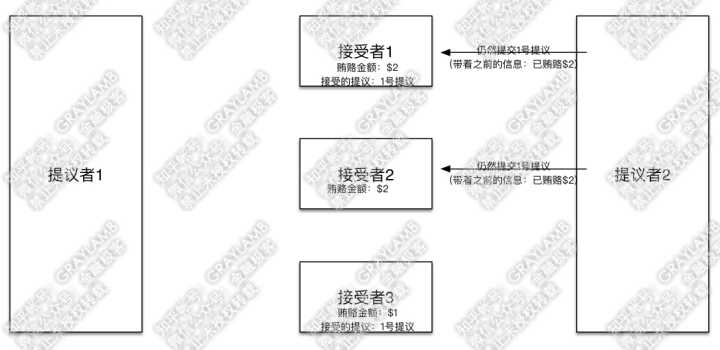
这时“提议者2”,拿到信息后,判断一下,目前贿赂过最高金额(即$1)的提议就是1号提议了,所以“提议者2”默默的把自己的提议改为与1号提议一致,然后开始向“接受者1”“接受者2”发起提议(提议内容仍然是1号提议),并带着信息:之前自己已贿赂过$2。
11)这时“接受者1”“接受者2”收到“提议者2”的提议后,照例先比对一下贿赂金额,比对发现“提议者2”之前已贿赂$2,并且自己记录的贿赂金额也是$2,所以接受他的提议,也就是都接受1号提议。
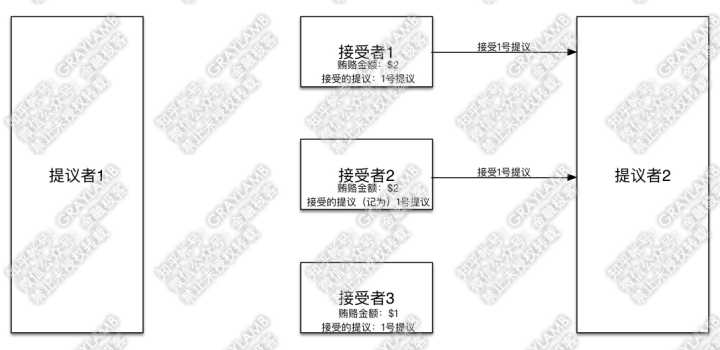
12)于是,“提议者2”也拿到了多数派的意见,最终通过的也是1号提议。
这里再多说一句:
回到上面的第5)步,如果“提议者2”第一次先去贿赂“接受者2”“接受者3”会发生什么?那很可能1号提议就不会成为最终选出的提议。因为当“提议者2”先贿赂到了“接受者2”“接受者3”,那等“提议者1”带着议题再去找这两位的时候,就会因为之前贿赂的钱少($1<$2)而被拒绝。
所以,这也就是刚才讲到可能存在博弈的地方:
a.“提议者1”要赶在“提议者2”贿赂到“接受者2”“接受者3”之前,让“接受者2”“接受者3”接受自己的意见,否则“提议者1”会因为钱少而被拒绝;
b.“提议者2”要赶在“提议者1”之前贿赂到“接受者”,否则“提议者2”即便贿赂成功,也要默默的将自己的提议改为“提议者1”的提议。但你往后推演会发现,无论如何,总会有一个“提议者”的提议获得多数票而胜出。
以上,只是把大致的Paxos算法的思路介绍了一下,因为情景实在太复杂,比如:“提议者”、“接受者”如果是4个、5个……,比如:“提议者”与“接受者”之间的交互谁先谁后,等等各类情况。
但是,其实都是能够严谨的推导出最后能够选出一个多数派的,不过篇幅就会太长了。大家有兴趣可以按照上面的思路,自己再模拟模拟“提议者”“接受者”数量或多或少,交互或先或后的各种情况,结果肯定是最终唯一一个提议会获得多数票而胜出。
https://www.zhihu.com/question/19787937
http://www.cnblogs.com/linbingdong/p/6253479.html