常见参数方程属
曲线的极坐标参数方程ρ=f(t),θ=g(t)。
圆的参数方程 x=a+r cosθ y=b+r sinθ(θ∈ [0,2π) ) (a,b) 为圆心坐标,r 为圆半径,θ 为参数,(x,y) 为经过点的坐标
椭圆的参数方程 x=a cosθ y=b sinθ(θ∈[0,2π)) a为长半轴长 b为短半轴长 θ为参数 [2]
双曲线的参数方程 x=a secθ (正割) y=b tanθ a为实半轴长 b为虚半轴长 θ为参数
抛物线的参数方程 x=2pt^2 y=2pt p表示焦点到准线的距离 t为参数
直线的参数方程 x=x'+tcosa y=y'+tsina,x',y'和a表示直线经过(x',y'),且倾斜角为a,t为参数
参数方程化为直角坐标方程的过程就是消参过程,常见方法有三种:
①代入法:利用解方程的技巧求出参数t,然后代入消去参数;
②三角法:利用三角恒等式消去参数;
③整体zhidao消元法:根据参数方程专本身的结构特征,从整体上消去。
参数方程在直角坐标系下的积分,可以将参数方程转化为直角方程然后积分:例一;或者直接写出直角坐标系下的积分式,然后用参数方程替代直角坐标系下的积分式和积分微元:例二;
2016数学二20题:
例一:
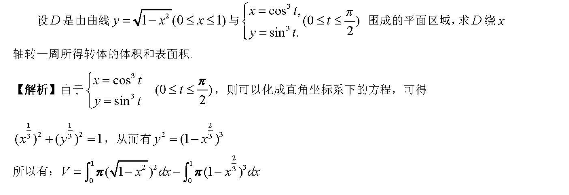
例二:

个人给出建议:用第二种方法,因为既然题目中给的是参数方程,那么一般情况下其直角坐标系下的方程用来计算不会太方便,即使转换成功了也比较考验积分能力。三角函数的积分因为有点火公式(华里士公式)的存在,变得相当简单。
