题目
Given a syntax tree (binary), you are supposed to output the corresponding infix expression, with parentheses reflecting the precedences of the operators.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N ( <= 20 ) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the i-th line corresponds to the i-th node) in the format:
data lef_child right_child
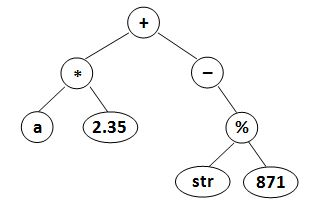
where data is a string of no more than 10 characters, lef_child and right_child are the indices of this node’s lef and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by -1. The figures 1 and 2 correspond to the samples 1 and 2, respectively

Output Specification:
For each case, print in a line the infix expression, with parentheses reflecting the precedences of the operators. Note that there must be no extra parentheses for the final expression, as is shown by the samples. There must be no space between any symbols.
Sample Input 1:
8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1
Sample Output 1:
(a+b)(c(-d))
Sample Input 2:
8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1
Sample Output 2:
(a*2.35)+(-(str%871))
题目分析
中缀表达式树,打印表达式
解题思路
1 保存中缀树
使用node数组保存中缀树,并在输入过程中,记录每个节点的父节点到数组father中
2 寻找根
遍历father数组,找出父节点为0的元素即为根
3 中序遍历,打印表达式
3.1 最外层无需括号,叶子节点无需括号
3.2 只要结点有孩子,就要在访问子孩子之前加(,之后加)
Code
#include <iostream>
using namespace std;
const int maxn = 25;
struct node {
char data[11];
int left;
int right;
};
node nds[maxn];
int father[maxn];
void in_order_travel(int v,int r) {
if(v==-1)return;
// 叶子结点无需括号
if(nds[v].left==-1&&nds[v].right==-1)printf("%s",nds[v].data);
else {
if(v!=r)printf("("); //根节点左孩子前无需括号
in_order_travel(nds[v].left,r);
printf("%s",nds[v].data);
in_order_travel(nds[v].right,r);
if(v!=r)printf(")"); //根节点右孩子后无需括号
}
}
int main(int argc,char * argv[]) {
int n;
scanf("%d",&n);
for(int i=1; i<=n; i++) {
scanf("%s %d %d",nds[i].data,&nds[i].left,&nds[i].right);
father[nds[i].left]=father[nds[i].right]=i;
}
// 查找根
int k=1;
while(k<=n&&father[k]!=0)k++;
// 中序遍历
in_order_travel(k,k);
return 0;
}