After finishing eating her bun, Alyona came up with two integers n and m. She decided to write down two columns of integers — the first column containing integers from 1 to n and the second containing integers from 1 to m. Now the girl wants to count how many pairs of integers she can choose, one from the first column and the other from the second column, such that their sum is divisible by 5.
Formally, Alyona wants to count the number of pairs of integers (x, y) such that 1 ≤ x ≤ n, 1 ≤ y ≤ m and 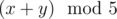 equals 0.
equals 0.
As usual, Alyona has some troubles and asks you to help.
The only line of the input contains two integers n and m (1 ≤ n, m ≤ 1 000 000).
Print the only integer — the number of pairs of integers (x, y) such that 1 ≤ x ≤ n, 1 ≤ y ≤ m and (x + y) is divisible by 5.
6 12
14
11 14
31
1 5
1
3 8
5
5 7
7
21 21
88
Following pairs are suitable in the first sample case:
for x = 1 fits y equal to 4 or 9;
- for x = 2 fits y equal to 3 or 8;
- for x = 3 fits y equal to 2, 7 or 12;
- for x = 4 fits y equal to 1, 6 or 11;
- for x = 5 fits y equal to 5 or 10;
- for x = 6 fits y equal to 4 or 9.
Only the pair (1, 4) is suitable in the third sample case.
题意:给你 n,m 1 ≤ x ≤ n, 1 ≤ y ≤ m 问有多少对x/y 使得(x+y)%5==0
题解:水
1 #include <bits/stdc++.h> 2 #define ll __int64 3 using namespace std; 4 int n,m; 5 int main() 6 { 7 scanf("%d %d",&n,&m); 8 ll ans=0; 9 for(int i=1;i<=n;i++) 10 { 11 int exm=i%5; 12 int re=5-exm; 13 if(m>=re){ 14 ans=ans+(m-re)/5; 15 ans++; 16 } 17 } 18 cout<<ans<<endl; 19 return 0; 20 }
Someone gave Alyona an array containing n positive integers a1, a2, ..., an. In one operation, Alyona can choose any element of the array and decrease it, i.e. replace with any positive integer that is smaller than the current one. Alyona can repeat this operation as many times as she wants. In particular, she may not apply any operation to the array at all.
Formally, after applying some operations Alyona will get an array of n positive integers b1, b2, ..., bn such that 1 ≤ bi ≤ ai for every 1 ≤ i ≤ n. Your task is to determine the maximum possible value of mex of this array.
Mex of an array in this problem is the minimum positive integer that doesn't appear in this array. For example, mex of the array containing 1, 3 and 4 is equal to 2, while mex of the array containing 2, 3 and 2 is equal to 1.
The first line of the input contains a single integer n (1 ≤ n ≤ 100 000) — the number of elements in the Alyona's array.
The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the elements of the array.
Print one positive integer — the maximum possible value of mex of the array after Alyona applies some (possibly none) operations.
5
1 3 3 3 6
5
2
2 1
3
In the first sample case if one will decrease the second element value to 2 and the fifth element value to 4 then the mex value of resulting array 1 2 3 3 4 will be equal to 5.
To reach the answer to the second sample case one must not decrease any of the array elements.
题意:给你n个数 每次操作只能减小某个数 经过一系列操作之后 使得没有出现的数的最小值尽量大
题解:水
1 #include <bits/stdc++.h> 2 #define ll __int64 3 using namespace std; 4 int n; 5 int a[100005]; 6 int main() 7 { 8 scanf("%d",&n); 9 for(int i=1;i<=n;i++) 10 scanf("%d",&a[i]); 11 sort(a+1,a+1+n); 12 int now=1; 13 for(int i=1;i<=n;i++) 14 { 15 if(now<=a[i]) 16 now++; 17 else 18 continue; 19 } 20 cout<<now<<endl; 21 return 0; 22 }
Alyona decided to go on a diet and went to the forest to get some apples. There she unexpectedly found a magic rooted tree with root in the vertex 1, every vertex and every edge of which has a number written on.
The girl noticed that some of the tree's vertices are sad, so she decided to play with them. Let's call vertex v sad if there is a vertex u in subtree of vertex v such that dist(v, u) > au, where au is the number written on vertex u, dist(v, u) is the sum of the numbers written on the edges on the path from v to u.
Leaves of a tree are vertices connected to a single vertex by a single edge, but the root of a tree is a leaf if and only if the tree consists of a single vertex — root.
Thus Alyona decided to remove some of tree leaves until there will be no any sad vertex left in the tree. What is the minimum number of leaves Alyona needs to remove?
In the first line of the input integer n (1 ≤ n ≤ 105) is given — the number of vertices in the tree.
In the second line the sequence of n integers a1, a2, ..., an (1 ≤ ai ≤ 109) is given, where ai is the number written on vertex i.
The next n - 1 lines describe tree edges: ith of them consists of two integers pi and ci (1 ≤ pi ≤ n, - 109 ≤ ci ≤ 109), meaning that there is an edge connecting vertices i + 1 and pi with number ci written on it.
Print the only integer — the minimum number of leaves Alyona needs to remove such that there will be no any sad vertex left in the tree.
9
88 22 83 14 95 91 98 53 11
3 24
7 -8
1 67
1 64
9 65
5 12
6 -80
3 8
5
The following image represents possible process of removing leaves from the tree:
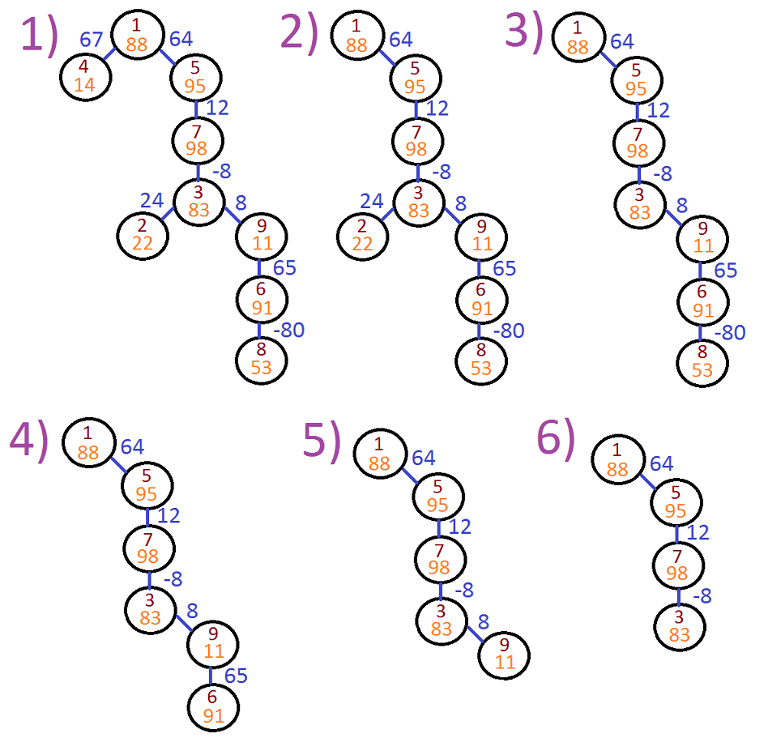
题意:给你一个树 有点权 边权 删除最少的叶子结点 使得 对于任意一个点到其子树中的点的路径边权和小于等与目标点的点权
题解:dfs处理 记录当前节点的祖先节点中到当前节点的路径边权和的最大值
1 #include <bits/stdc++.h> 2 #define ll __int64 3 using namespace std; 4 ll n; 5 ll a[100005]; 6 ll p[100005]; 7 ll in[100005]; 8 ll out[100005]; 9 ll d[100005]; 10 map<ll,ll> mp; 11 ll nedge=0; 12 ll dfn=0; 13 ll re=0; 14 struct node 15 { 16 ll to; 17 ll pre; 18 ll we; 19 }N[200005]; 20 void add(ll pre,ll to,ll we) 21 { 22 nedge++; 23 N[nedge].to=to; 24 N[nedge].we=we; 25 N[nedge].pre=p[pre]; 26 p[pre]=nedge; 27 } 28 void getdfs(ll root,ll sum,ll now) 29 { 30 in[root]=++dfn; 31 d[root]=max(sum,now); 32 sum=d[root]; 33 mp[root]=1; 34 for(int i=p[root];i;i=N[i].pre){ 35 if(mp[N[i].to]) 36 continue; 37 getdfs(N[i].to,sum+N[i].we,N[i].we); 38 } 39 out[root]=dfn; 40 } 41 void dfs(ll root) 42 { 43 mp[root]=1; 44 for(int i=p[root];i;i=N[i].pre){ 45 if(mp[N[i].to]) 46 continue; 47 if(d[N[i].to]>a[N[i].to]) 48 { 49 re=re+out[N[i].to]-in[N[i].to]+1; 50 continue ; 51 } 52 dfs(N[i].to); 53 } 54 } 55 int main() 56 { 57 ll r,w; 58 memset(p,0,sizeof(p)); 59 scanf("%I64d",&n); 60 for(ll i=1;i<=n;i++) 61 scanf("%I64d",&a[i]); 62 for(ll i=2;i<=n;i++) 63 { 64 scanf("%I64d %I64d",&r,&w); 65 add(i,r,w); 66 add(r,i,w); 67 } 68 getdfs(1,0ll,0ll); 69 mp.clear(); 70 dfs(1); 71 printf("%I64d ",re); 72 return 0; 73 }