傅里叶级数（FS）以及FT、DTFT、DFS和DFT

• 傅里叶级数（FS）

周期为 T 的函数$f(t), omega=frac{2pi}{T}$. 正交基为${ e^{jnomega t} },n=0,pm1,pm2,cdots$。

$$
 f(t)=sum_{n=-infty}^{infty}C_ne^{-jomega nt} \
C_n=frac{<f(t),e^{jnomega t}>}{<e^{jnomega t},e^{jnomega t}>}=frac{int_Tf(t)e^{-jnomega t}dt}{int_T e^{jnomega t}e^{-jnomega t}dt}=frac{1}{T}int_Tf(t)e^{-jnomega t}dt
$$

• 连续时间的傅里叶变换（FT）

$$
F(omega)=int_{-infty}^infty f(t)e^{-jomega t}dt \
f(t)=frac{1}{2pi}int_{-infty}^infty F(omega)e^{j\,omega t}domega
$$

• 离散时间序列的傅里叶变换（DTFT)

它用于离散非周期序列分析对应频域连续周期(周期为 $2pi$)，条件是 $x(n)$ 绝对可和 或者 能量有限，即 $sum_{n=-infty}^{infty}|x(n)|< infty  qquad  sum_{n=-infty}^{infty}|x(n)|^2< infty $。

$$   X(e^{jomega})=sum_{n=-infty}^{infty}x(n)e^{-jomega \,n}     qquad   (1)       \ x(n) = frac{1}{2pi}int_{-pi}^{pi}X(e^{jomega})e^{jomega n}domega   qquad  (2)    $$     

式(1)中，$omega$ 为数字角频率，它是模拟域频率 $Omega$ 对采样频率 $f_s$ 的归一化，即 $omega = Omega T_s = Omega / f_s $

• Z变换

由$quad z = e^{jomega} $代入上式得

$$  X(z) = sum_{n=-infty}^{infty}x(n)z^{-n}  $$

• 周期序列的离散傅里叶级数（DFS）

x(n) 是周期为 N 的周期序列，可以看做X(k)的傅里叶级数频域展开，离散周期 ---> 周期离散，周期都为N。
$$   ilde X (k)=sum_{n=0}^{N-1} ilde x(n)e^{-jfrac{2pi}{N}nk}=sum_{n=0}^{N-1}  ilde x(n)W_{N}^{nk} qquad qquad k in mathbb{Z} \    ilde x(n)=frac{1}{N}sum_{k=0}^{N-1}  ilde X(k)e^{jfrac{2pi}{N}nk}=frac{1}{N}sum_{k=0}^{N-1}  ilde X(k)W_N^{-nk}  qquad qquad n in mathbb{Z} \  W_N=e^{-jfrac{2pi}{N}}                          $$

• 有限长序列的离散傅里叶变换（DFT）

x(n) 为有限长序列，长度为 N 。其他值都为 0 。

$$  X(k)=sum_{n=0}^{N-1}x(n)W_N^{-nk} qquad 0leqslant k leqslant N-1  \  x(n) = frac{1}{N}sum_{k=0}^{N-1}X(k)W_N^{-nk} qquad 0leqslant n leqslant N-1  $$

• DFT 与 DTFT 、z变换 的关系

$$  X(k) =X(e^{jomega})|_{omega =frac{2pi}{N}k}  \  X(k) = X(z)|_{z=W_N^{-k}}  $$

 

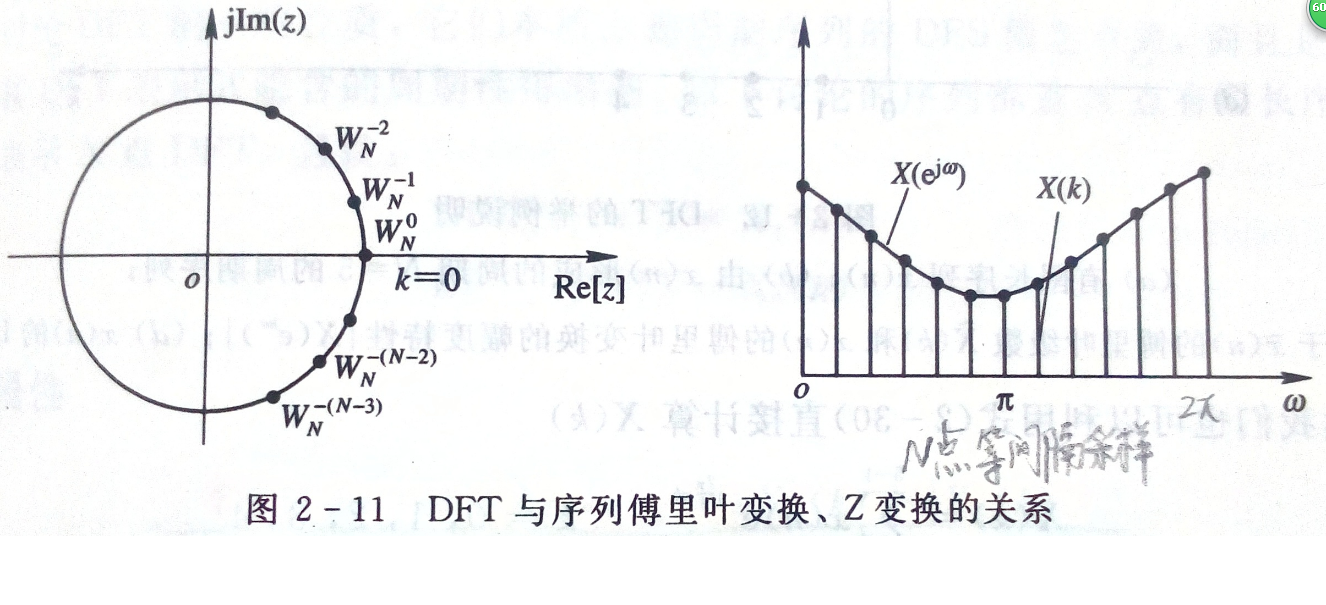
 参考：http://www.cnblogs.com/BitArt/archive/2012/11/24/2786390.html

---

Matlab仿真信号的抽样，CFT，DFT 和 FFT

ts=0.5; %采样时间间隔
df=1.0;
fs = 1/ts;  %采样频率
n2 = 50/ts;  %time=[0,50]之间采样
n1 = fs/df;
N = 2^(max(nextpow2(n1),nextpow2(n2))); %nextpow2(N) returns the first P such that 2.^P >= abs(N).  
          %当序列是2的幂次方时，FFT高效
df = fs/N;  %设置分辨率
t = 0:0.01:50;
y = cos(2/5*pi*t);
subplot(2,2,1);
plot(t,y,'k:');  %绘制余弦信号
hold on
t2=0:ts:50;
y2=cos(2/5*pi*t2);
stem(t2,y2,'k');     % 画火柴杆图，对余弦信号抽样
axis([0 10 -1.2,1.2]);
title('抽样信号: 
m x_{s}(t)');
xlabel('t');
line([0 10],[0 0],'color',[0 0 0]);
hold off

k=-N:N;
w = df*k;
Y = 0.01*y*exp(-j*2*pi*t'*w);% 计算CFT
Y=abs(Y);
subplot(2,2,2);
plot(w,Y,'k');
axis([-fs/2-0.5,fs/2+0.5,0,8*pi+0.5]);
title('连续傅里叶变换: X(f)');
xlabel('f');

subplot(2,2,3);
Y1=y2*exp(-j*2*pi*t2'*w); % 计算离散傅里叶变换
Y1=Y1/fs;
plot(w,abs(Y1),'k');
title('离散傅里叶变换 
m X_{s}(f)');
xlabel('f');
axis([-fs/2-1,fs/2+1,0,8*pi+0.5]);

Y2=fft(y2,N); %使用FFT计算离散傅里叶变换
Y2=Y2/fs;
f=[0:df:df*(N-1)]-fs/2; %调整频率坐标
subplot(2,2,4);
plot(f,fftshift(abs(Y2)),'k');
axis([-fs/2-0.5,fs/2+0.5,0,8*pi+0.5]);
title('快速傅里叶变换：
m X_{s}(f) ');
xlabel('f');

　　

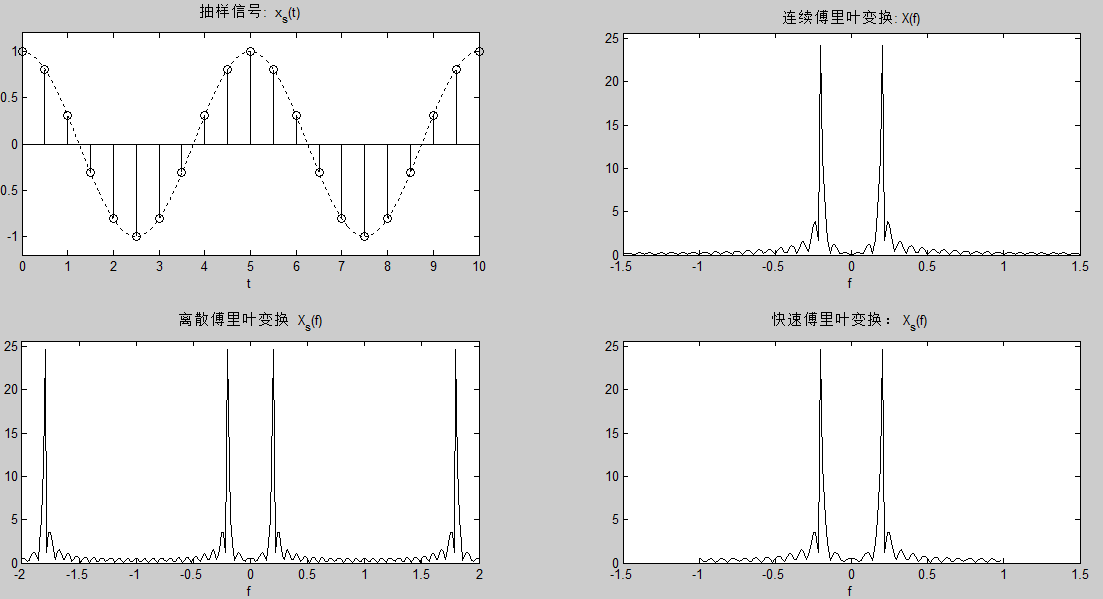
 由此可见，FFT 可以很好地表现 CFT 的频谱图。计算又快，所以用抽样信号的 FFT 代替 连续信号的 CFT。