简介
众所周知啊,与它齐名的还有个树状数组,那是一个简单亿倍的东西,问题不大。
线段树、是一种二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。时间复杂度为O(logN)。而未优化的空间复杂度为2N,实际应用时一般还要开4N的数组以免越界(毒瘤到炸),因此有时需要离散化让空间压缩。
这种东西啊,一般都处理可以运用结合律的东西(对,就是小学生都会的东西例如区间最值问题,或者是区间和什么的
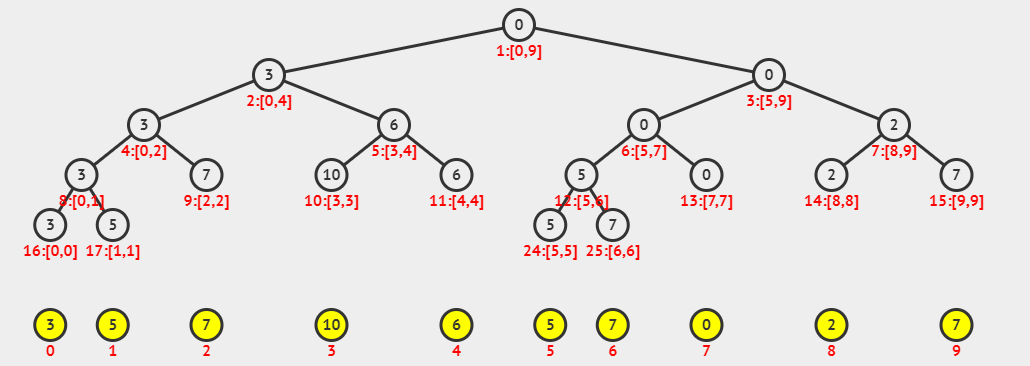
例如这个,叶子结点就是单个的数,其中每个非叶子节点都是一段区间,并且也就是他儿子节点信息的整合(比如这里是min的问题)由此可见,线段树是二叉树。
建树
利用二叉树的性质可知一个点x的左右儿子分别是x*2和x*2+1,所以利用这个性质我们求出儿子
int ls(int p){return p<<1;}//左儿子 int rs(int p){return p<<1|1;}//又儿子
因为这个数是从下往上整理的,所以我们就可以搜索这个二叉树,一旦到了叶子结点,我们就可以给它赋值,等到一个节点的子节点做完了后,我们就可以整理
void push_up(int p) { ans[p]=ans[ls(p)]+ans[rs(p)];//整理子节点 } void build(int p,int l,int r)//节点编号和左右区间 { tag[p]=0;//标记清空 if(l==r)//叶子结点 { ans[p]=a[l];//赋值 return; } int mid=(l+r)>>1;//二分递归左右儿子 build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p);//整理信息 }
现在就是区间修改了(单点修改就是区间长为1的特殊的区间修改
这里要引入一个懒标记(lazy
为什么呢,因为如果每次区间修改都递归到叶子结点然后再向上传,这个时间复杂度是极高的
所以当我们找到修改的区间后,打上标记,后面做操作
因为当这个区间的值暂时不用的时候,下一次再修改这个区间,就可以直接累加,两次或者多次操作就可以成功地合并成一次操作,时间复杂度也就大大降低的,但是怎么操作呢?
void f(ll p,ll l,ll r,ll k) { tag[p]+=k;//记录标记 ans[p]+=k*(r-l+1);//并且更改值 } void push_down(ll p,ll l,ll r) { ll mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]=0;//标记下传,标记清空 } void add(int nl,int nr,int l,int r,int p,int k) {//修改左右区间,当前左右区间,当前节点编号,修改的值 if(l>=nl&&r<=nr)//找到区间我们就 { tag[p]+=k;//直接打标记 ans[p]+=k*(r-l+1);//因为区间内每个点都加上k,区间值也就元素个数*k return; } push_down(p,l,r);//这里有一个向下传递标记的作用,因为能到这里的区间有可能有一部分是要修改的,也就是说对于现在的这个区间 //是有影响的,,并且后面的查询有可能会用到这个值,所以要更新 ll mid=(l+r)>>1;//便利子节点 if(nl<=mid)add(nl,nr,l,mid,ls(p),k); if(mid<nr)add(nl,nr,mid+1,r,rs(p),k); push_up(p);//更新当前结点的信息 }
为什么修改的时候要下传懒标记并且更新呢

当我们看当前区间的时候,要传到子区间,是因为当查询的时候,那一段并没有直接更改值(红色的因为是更改的,所以直接ans变了),为了保证黄色区间的正确性,我们就需要从子节点整合,而子节点恰好需要上面的节点来传递标记更新
而push_down在回溯之前是因为这样才能在向下的时候顺便传递懒标记,而push_up同理,也就是在回溯的时候顺便整理
询问和修改差不多,也是搜索区间直接返回值
ll answer(ll nl,ll nr,ll l,ll r,ll p) { ll res=0; if(nl<=l&&r<=nr)return ans[p];//在区间内直接返回 push_down(p,l,r);//以防懒标记未下传,可以想象成这个先answer一步整理数据(因为区间内改可以直接改,不用push_up) ll mid=(l+r)>>1;//左右儿子 if(nl<=mid)res+=answer(nl,nr,l,mid,ls(p)); if(mid<nr)res+=answer(nl,nr,mid+1,r,rs(p)); return res; }
这个就是线段树的基本操作
1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 const int N=1000005<<1; 5 ll n,m; 6 ll ans[N]; 7 ll tag[N]; 8 ll a[N]; 9 int ls(int p){return p<<1;} 10 int rs(int p){return p<<1|1;} 11 void push_up(ll p){ans[p]=ans[ls(p)]+ans[rs(p)];} 12 void f(ll p,ll l,ll r,ll k) 13 { 14 tag[p]+=k; 15 ans[p]+=k*(r-l+1); 16 } 17 void push_down(ll p,ll l,ll r) 18 { 19 ll mid=(l+r)>>1; 20 f(ls(p),l,mid,tag[p]); 21 f(rs(p),mid+1,r,tag[p]); 22 tag[p]=0; 23 } 24 void build(ll p,ll l,ll r) 25 { 26 tag[p]=0; 27 if(l==r) 28 { 29 ans[p]=a[l]; 30 return; 31 } 32 ll mid=(l+r)>>1; 33 build(ls(p),l,mid); 34 build(rs(p),mid+1,r); 35 push_up(p); 36 } 37 void add(ll nl,ll nr,ll l,ll r,ll p,ll k) 38 { 39 if(l>=nl&&r<=nr) 40 { 41 tag[p]+=k; 42 ans[p]+=k*(r-l+1); 43 return; 44 } 45 push_down(p,l,r); 46 ll mid=(l+r)>>1; 47 if(nl<=mid)add(nl,nr,l,mid,ls(p),k); 48 if(mid<nr)add(nl,nr,mid+1,r,rs(p),k); 49 push_up(p); 50 } 51 ll answer(ll nl,ll nr,ll l,ll r,ll p) 52 { 53 ll res=0; 54 if(nl<=l&&r<=nr)return ans[p]; 55 push_down(p,l,r); 56 ll mid=(l+r)>>1; 57 if(nl<=mid)res+=answer(nl,nr,l,mid,ls(p)); 58 if(mid<nr)res+=answer(nl,nr,mid+1,r,rs(p)); 59 return res; 60 } 61 int main() 62 { 63 scanf("%lld%lld",&n,&m); 64 for(int i=1;i<=n;i++)scanf("%lld",&a[i]); 65 build(1,1,n); 66 while(m--) 67 { 68 ll p,l,r,k; 69 scanf("%lld",&p); 70 switch(p) 71 { 72 case 1:{ 73 scanf("%lld%lld%lld",&l,&r,&k); 74 add(l,r,1,n,1,k); 75 break; 76 } 77 case 2:{ 78 scanf("%lld%lld",&l,&r); 79 printf("%lld ",answer(l,r,1,n,1)); 80 break; 81 } 82 } 83 } 84 return 0; 85 }
区间乘法
这里就只加了个区间乘法的操作。所以要多维护一个标记,并且要考虑标记之间互相的影响
这个节点的加法标记为t[p].tag 乘法标记为t[p].tagup 区间和为t[p].ans
然后我们计算的时候要考虑先后顺序(一般我们都是先乘后加
假设要乘上一个数k1和加上一个数k2
t[p].tagup*=k1;//乘法标记继承 t[p].tag=(t[p].tag*k1)+k2;//加法标记继承,因为是先乘后加 t[p].ans=(t[p].ans*k)+(r-l+1)*k2;//区间和计算
有些人可能会疑问运算先后顺序对程序会不会造成影响,事实是不会的,因为不同的运算顺序这里的写法也不一样
如果是先加上k1然后乘上k2
t[p].tag=(t[p].tag+k1)*k2; t[p].tagup*=k2; t[p].ans=(r-l+1)*k1+(t[p].ans+(r-l+1)*k1)*k2;
就有亿点麻烦(应该没打错吧
然后剩下的操作还是一样的,问题不大
1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 const int N=1000010; 5 int n,m,mod; 6 int tagup[N],tag[N],ans[N],a[N]; 7 int l_[N],r_[N]; 8 int ls(int p){return p<<1;} 9 int rs(int p){return p<<1|1;} 10 void f(int p,int up,int k) 11 { 12 (tagup[p]*=up)%=mod; 13 tag[p]=(tag[p]*up+k)%mod; 14 ans[p]=ans[p]*up%mod+k*(r_[p]-l_[p]+1)%mod; 15 16 } 17 void push_down(int p,int l,int r) 18 { 19 f(ls(p),tagup[p],tag[p]); 20 f(rs(p),tagup[p],tag[p]); 21 tagup[p]=1; 22 tag[p]=0; 23 } 24 void push_up(int p){ans[p]=(ans[ls(p)]+ans[rs(p)])%mod;} 25 void build(int p,int l,int r) 26 { 27 tagup[p]=1;//注意初始化 28 l_[p]=l; 29 r_[p]=r; 30 if(l==r) 31 { 32 ans[p]=a[l]; 33 return; 34 } 35 int mid=(l+r)>>1; 36 build(ls(p),l,mid); 37 build(rs(p),mid+1,r); 38 push_up(p); 39 } 40 void addup(int nl,int nr,int l,int r,int p,int k) 41 { 42 if(nl<=l&&r<=nr) 43 { 44 f(p,k,0);//乘上一个数就等于加法标记为0的时候 45 return; 46 } 47 push_down(p,l,r); 48 int mid=(l+r)>>1; 49 if(mid>=nl)addup(nl,nr,l,mid,ls(p),k); 50 if(mid<nr)addup(nl,nr,mid+1,r,rs(p),k); 51 push_up(p); 52 } 53 void add(int nl,int nr,int l,int r,int p,int k) 54 { 55 if(nl<=l&&r<=nr) 56 { 57 f(p,1,k);//加上一个数也就是乘法标记为1 58 return; 59 } 60 push_down(p,l,r); 61 int mid=(l+r)>>1; 62 if(mid>=nl)add(nl,nr,l,mid,ls(p),k); 63 if(mid<nr)add(nl,nr,mid+1,r,rs(p),k); 64 push_up(p); 65 } 66 int getsum(int nl,int nr,int l,int r,int p) 67 { 68 if(nl<=l&&r<=nr)return ans[p]; 69 int res=0; 70 push_down(p,l,r); 71 int mid=(l+r)>>1; 72 if(mid>=nl)res+=getsum(nl,nr,l,mid,ls(p)); 73 if(mid<nr)res+=getsum(nl,nr,mid+1,r,rs(p)); 74 return res%mod; 75 } 76 signed main() 77 { 78 scanf("%lld%lld%lld",&n,&m,&mod); 79 for(int i=1;i<=n;i++) 80 scanf("%lld",&a[i]); 81 build(1,1,n); 82 while(m--) 83 { 84 int k,x,y,z; 85 scanf("%lld",&k); 86 switch(k) 87 { 88 case 1:{ 89 scanf("%lld%lld%lld",&x,&y,&z); 90 addup(x,y,1,n,1,z); 91 break; 92 } 93 case 2:{ 94 scanf("%lld%lld%lld",&x,&y,&z); 95 add(x,y,1,n,1,z); 96 break; 97 } 98 case 3:{ 99 scanf("%lld%lld",&x,&y); 100 printf("%lld ",getsum(x,y,1,n,1)%mod); 101 break; 102 } 103 } 104 } 105 return 0; 106 }
区间最值操作
0,x,y,t需要你在x到y的区间里把每一个大于t的数变成t,也就是a[i]=min(a[i],t)(x<=i<=y) 1,x,y需要你求出区间内的最大值 2,x,y需要你求出区间内的和
之前的区间加法我们可以直接更新区间和,但是这里显然要找一种其他的方法来达到快速更新区间和,从而降低复杂度
这里首先想到的就是维护每个区间的最大值mx,严格次大值se和最大值的个数cnt,假设更改的为k
当k>mx时直接退出
当se<k<mx时直接修改最大值,然后区间减少的就是(mx-k)*cnt,并打上标记
当k<=se时,不能立即更新,就递归到子树即可
#include<iostream> #define int long long using namespace std; const int N=4e6+10; int t,n,m; int tag[N],MAX[N],MAX_[N];//标记,最大值,严格次大值 int ans[N];//区间和 int cnt[N];//最大值个数 inline int ls(int p){return p<<1;} inline int rs(int p){return p<<1|1;} inline void push_up(int p) { if(MAX[ls(p)]>MAX[rs(p)]) { MAX[p]=MAX[ls(p)]; cnt[p]=cnt[ls(p)]; MAX_[p]=max(MAX[rs(p)],MAX_[ls(p)]); } else if(MAX[ls(p)]<MAX[rs(p)]) { MAX[p]=MAX[rs(p)]; cnt[p]=cnt[rs(p)]; MAX_[p]=max(MAX[ls(p)],MAX_[rs(p)]); } else //还是要判断左右儿子最大值都一样,要合并个数的 { MAX[p]=MAX[ls(p)]; cnt[p]=cnt[ls(p)]+cnt[rs(p)]; MAX_[p]=max(MAX_[ls(p)],MAX_[rs(p)]); } ans[p]=ans[ls(p)]+ans[rs(p)]; } void f(int p,int l,int r,int k) { if(k>=MAX[p])return;//大于最大值退出 if(k>=MAX_[p]) { ans[p]+=(k-MAX[p])*cnt[p]; MAX[p]=tag[p]=k;//打标记 } } void push_down(int p,int l,int r) { if(tag[p]==1e9)return; int mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]==1e9;//清空标记 } void build(int p,int l,int r) { tag[p]=1e9; MAX[p]=-1; MAX_[p]=-1e9;//一定要 初始值 cnt[p]=1; if(l==r) { scanf("%lld",&ans[p]); MAX[p]=ans[p]; return ; } int mid=(l+r)>>1; build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p); } void turnmin(int nl,int nr,int l,int r,int p,int k) { if(k>=MAX[p])return ; if(nl<=l&&r<=nr&&k>MAX_[p]) { f(p,l,r,k); return; } push_down(p,l,r); int mid=(l+r)>>1; if(mid>=nl)turnmin(nl,nr,l,mid,ls(p),k); if(mid<nr)turnmin(nl,nr,mid+1,r,rs(p),k); push_up(p); } int getsum(int nl,int nr,int l,int r,int p) { if(nl<=l&&r<=nr)return ans[p]; int res=0; push_down(p,l,r); int mid=(l+r)>>1; if(mid>=nl)res+=getsum(nl,nr,l,mid,ls(p)); if(mid<nr)res+=getsum(nl,nr,mid+1,r,rs(p)); return res; } int getmax(int nl,int nr,int l,int r,int p) { if(nl<=l&&r<=nr)return MAX[p]; int res=-1e9; push_down(p,l,r); int mid=(l+r)>>1; if(mid>=nl)res=max(res,getmax(nl,nr,l,mid,ls(p))); if(mid<nr)res=max(res,getmax(nl,nr,mid+1,r,rs(p))); return res; } signed main() { scanf("%lld",&t); while(t--) { scanf("%lld%lld",&n,&m); build(1,1,n); while(m--) { int k,x,y,z; scanf("%lld",&k); switch(k) { case 0:{ scanf("%lld%lld%lld",&x,&y,&z); turnmin(x,y,1,n,1,z); break; } case 1:{ scanf("%lld%lld",&x,&y); printf("%lld ",getmax(x,y,1,n,1)); break; } case 2:{ scanf("%lld%lld",&x,&y); printf("%lld ",getsum(x,y,1,n,1)); break; } } } } return 0; }
加上区间加减
问题不大,多一个标记,加的时候最大值次大值全部也要加就行了,然后把区间和改一改
大乱炖(确信
1.给一 个区间[L,R]加上一个数x 2.把个区间[L,R] 里小于x的数变成x 3.把一个区间[L,R] 里大于x的数变成x 4.求区间[L,R]的和 5.求区间[L,R]的最大值 6.求区间[L,R]的最小值