吴恩达机器学习4

逻辑回归

逻辑回归是一种用来解决当输出的y全部都是1或者0这种监督学习的机器学习算法。其目标就是最小化预测值和训练集之间的错误。

举个栗子：猫和没有猫

通过以向量x形式给出的一张图片，我们的目标就是判断这张图片中有没有猫

              给x,y'=P(y=1|x)  其中 0<=y'<=1

在逻辑回归中我们所需要利用的参数有：

　　1.输入特征向量:x∈R^nx,其中nx表示特征的数目

        2.训练的集合：y∈0,1

       3.权值 ：W∈R^nx,其中nx表示特征的数目

       4.偏值：b∈R

       5.输出：y∈σ(W^Tx+b)

      6.Sigmoid函数：s=σ(W^Tx+b)=σ(z)=1/(1+e^-z)

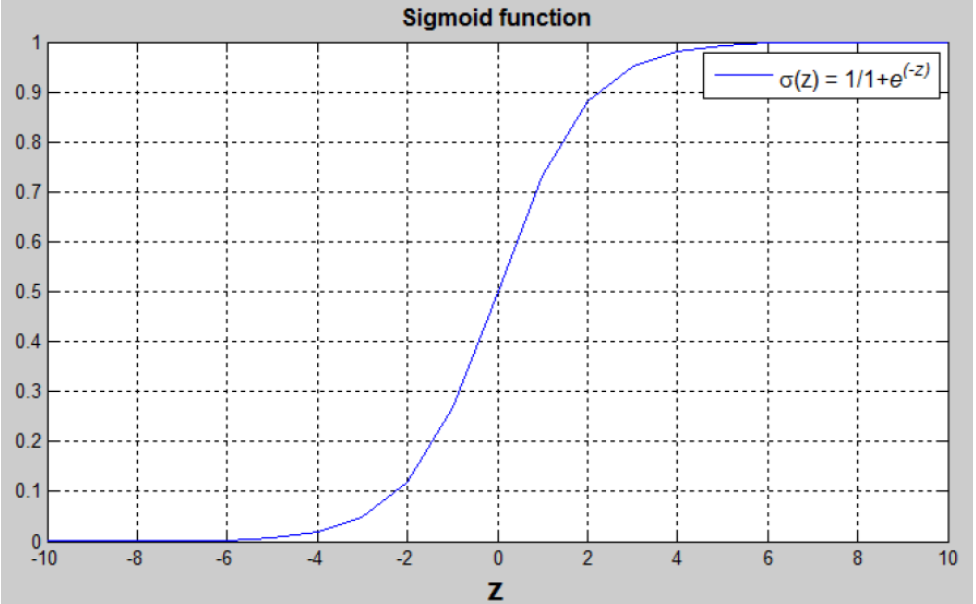
(W^Tx+b)是一个线性函数（ax+b），但是因为我们想找一个在【0,1】中更大概率的值，需要Sigmoid函数来进行转换；转换出来的值在【0,1】之间（如上图所示）

从上图中我们可以看到一些特征：

     1.如果z是一个特别大的正数，则σ（z）=1

     2.如果z是一个特别小的负数，则σ（z）=0

     3.如果z=0，则σ（z）=0.5

逻辑回归：成本函数

为了更好的训练W和b，我们需要定义一个成本函数

正如上面所示：

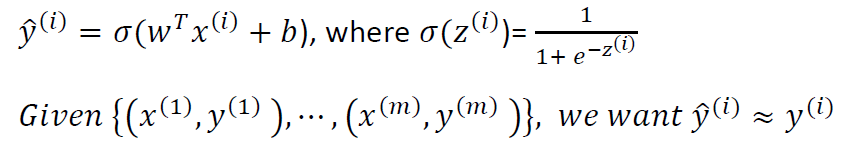
首先定义针对每一个样本的损失函数：

损失函数通常用来衡量我们通过模型的预测值（y'⁽ⁱ⁾）和真正输出的输出值(y⁽ⁱ⁾)。

换句话说，损失函数是针对每一个样本的错误表示

我们可以通过第一种方式来定义损失函数

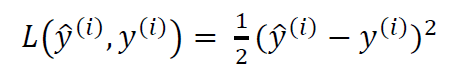
但是这种定义方式通常会导致损失函数不是凸函数，这样就无法寻找最低的损失函数。所以，我们通常采用另外一种方式来定义损失函数：

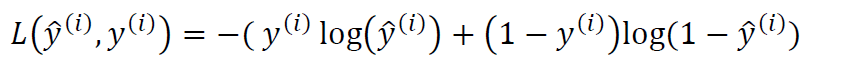
针对这种损失函数的定义，我们可以发现：

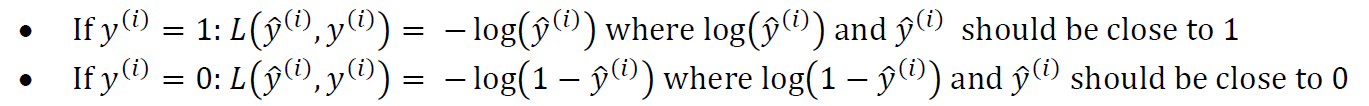
成本函数：

    成本函数是在训练集中所有的损失函数的值的平均。我们就是寻找最好的W和b来最小化这个成本函数，下面便是成本函数的定义