四阶龙格库塔法matlab解微分方程组

这是我在学习飞行器制导与控制时的课程作业。用四阶龙格库塔法解微分方程组。我一开始的想法是分别利用龙格库塔法解每一个微分方程，但变量很多，算法会比较复杂。后来明白可以把多变量看作是一个变量，利用matlab的feval函数进行代入变量的函数运算。

matlab中feval函数的作用：feval(f,x,y)；将x，y代入函数f中。

四阶龙格-库塔法：

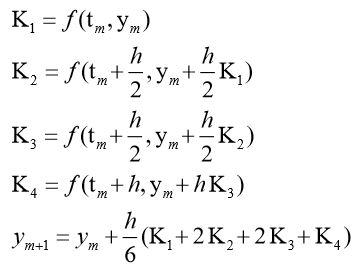
需要解的四个微分方程组为：

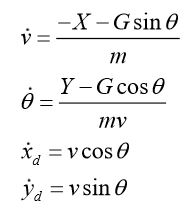
算法代码：

主函数main.m

main.m
clear all;
clc;
%% 定义初始参数
M0=2;            %马赫数
h0=5000;       %初始高度
theta0=-30*pi/180;    %初始弹道倾角，注意度数的表示
a=340;            %音速
g0=9.81;
%% 运算
v0=M0*a;
y0=[v0;theta0;0;h0];
h=0.01;   %步长
t0=0;
t1=200;
[finaltime,n,y,t] = RK4(@equations,y0,h,t0,t1);
%% 显示结果
title('弹道曲线');
plot(y(3,1:n),y(4,1:n));
xlabel('x/m');ylabel('h/m');
figure;
title('速度变化曲线');
plot(t(1:n),y(1,1:n));
xlabel('t/s');ylabel('v/(m/s)');
figure;

四阶龙格-库塔法RK4.m

function [finaltime,n,y,t] = RK4(f,y0,h,t0,t1)
%龙格库塔四阶
%   f:微分方程组
%   y0:[v;theta;x;h]初始值
%   h:步长
%   t0-t1:时间区间

t=t0:h:t1;
y=zeros(length(y0),length(t));
y(:,1)=y0;
flag=1;
n=1;
while(flag)           %判断导弹是否落地
    if (y(4,n)>0)
        k1=feval(f,t(n),y(:,n));
        k2=feval(f,t(n)+h/2,y(:,n)+h/2*k1);
        k3=feval(f,t(n)+h/2,y(:,n)+h/2*k2);
        k4=feval(f,t(n)+h,y(:,n)+h*k3);
        y(:,n+1)=y(:,n)+(h/6)*(k1+2*k2+2*k3+k4);
        n=n+1;
    else
        finaltime=t(n-1);
        flag=0;
     end
end

end

导弹质点运动的动力学微分方程组equations.m

function f= equations(t,y)
% 四个微分方程组
%   t为时间
%   y=[v;theta;x;h]
m=260;         %质量
s=0.24;           %参考面积
a=340;            %音速
alpha=2;       %攻角
g0=9.81;

M=y(1)/a;
G=m*g0;
rho=1.225*exp(-0.00015*y(4));

Cx=[M^2,M,1]*[0.0002, 0.0038, 0.1582;
                           -0.0022, -0.0132, -0.8520;
                           0.0115, -0.0044, 1.9712;]*[alpha^2,alpha,1]';
X=Cx*1/2*rho*(y(1)^2)*s;
Cy=[M^2,M,1]*[-0.026,0.0651,0.4913]'*alpha;
Y=Cy*1/2*rho*(y(1)^2)*s;

f(1)=-X/m-G*sin(y(2))/m;
f(2)=Y/(m*y(1))-G*cos(y(2))/(m*y(1));
f(3)=y(1)*cos(y(2));
f(4)=y(1)*sin(y(2));
f=f(:);
end