递归算法

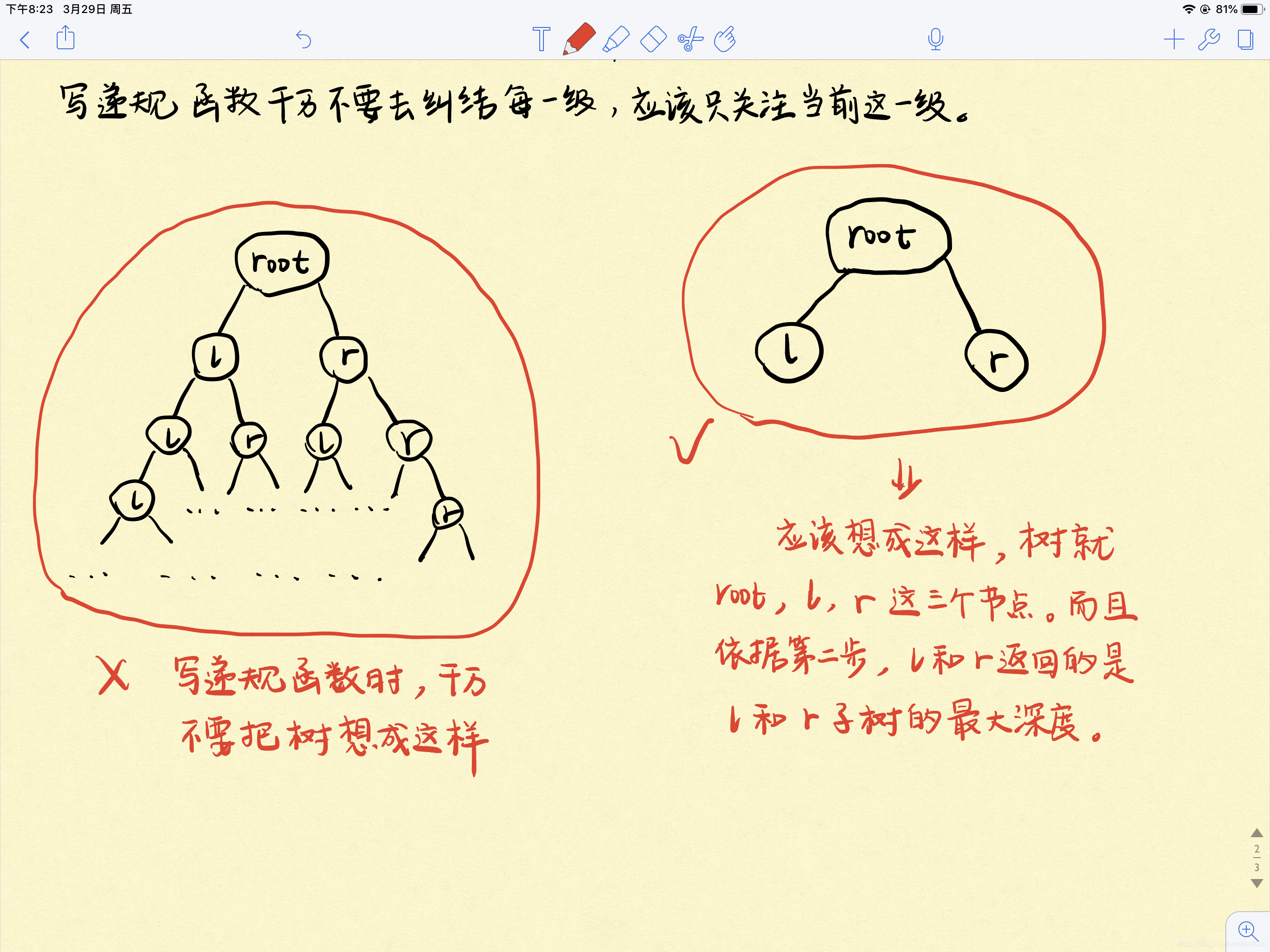
什么是递归

递归是一个反复调用自身的过程，这就说明它每一级的功能都是一样的，因此我们只需要关注一级递归的解决过程即可。

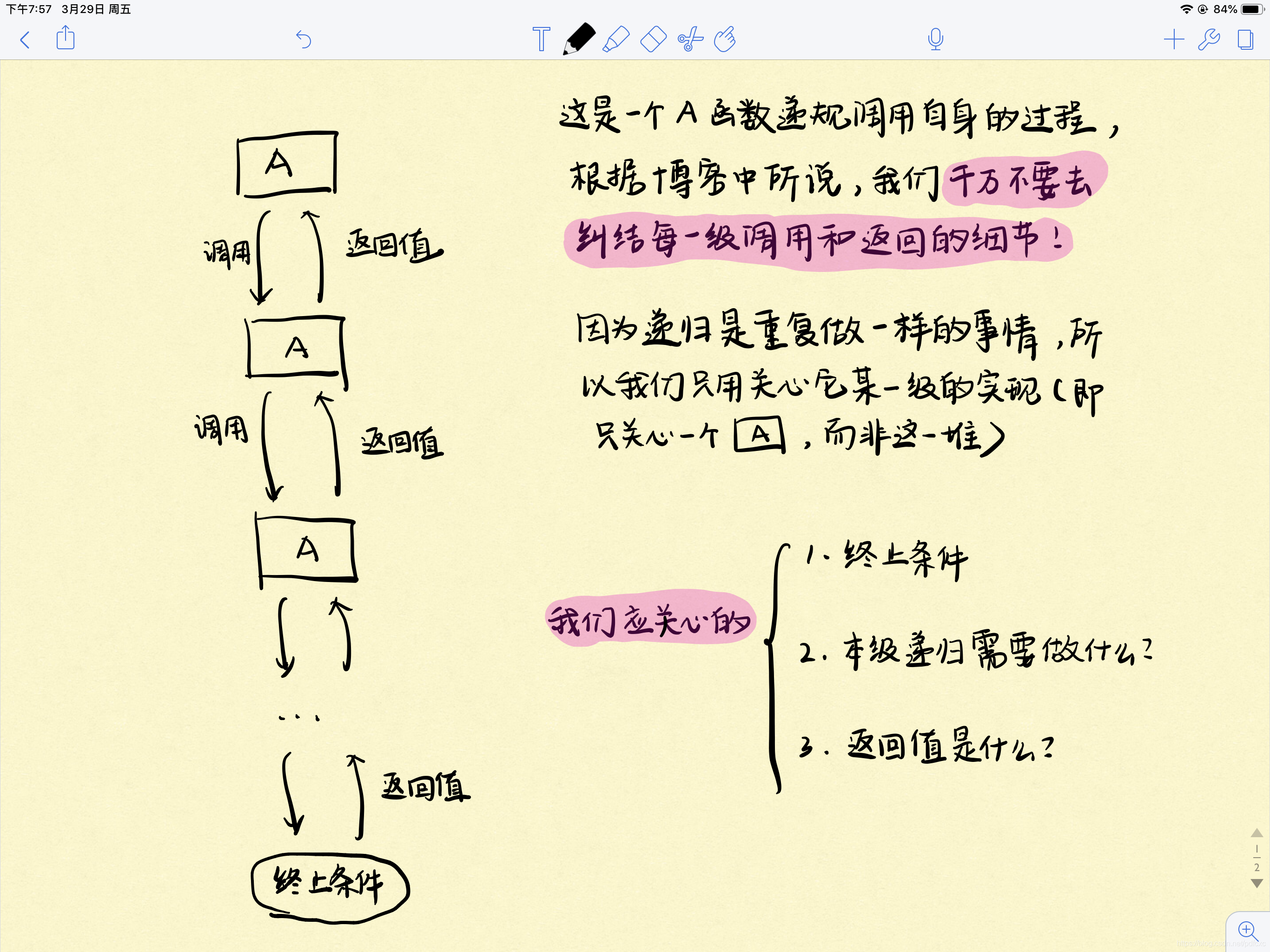
如上图所示，我们需要关心的主要是以下三点

• 整个递归的终止条件。
• 一级递归需要做什么？
• 应该返回给上一级的返回值是什么？

因此，也就有了我们解递归题的三部曲：

1. 找整个递归的终止条件：递归应该在什么时候结束？

2. 找返回值：应该给上一级返回什么信息？

3. 本级递归应该做什么：在这一级递归中，应该完成什么任务？

这就是以后递归秒杀算法题的依据和思路。

举例

二叉树的最大深度

class Solution{
  public int maxDepth(TreeNode root) {
    //1、终止条件
    if(root == null) return 0;
    
    //2、递归做什么,root左右子树的最大深度
    int leftDepth = maxDepth(root.left);
    int rightDepth = maxDepth(root.right);

    //3、返回上一级什么信息;返回的是左右子树的最大深度+1
    return Math.max(leftDepth, rightDepth) + 1;
    
  }
}

简洁的代码：

class Solution{
  public int maxDepth(TreeNode root) {
    return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
  }
}

两两交换链表中的节点

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1：

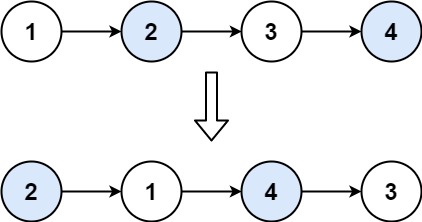
输入：head = [1,2,3,4]
输出：[2,1,4,3]

直接上三部曲模版：

1. 找终止条件。 什么情况下递归终止？没得交换的时候，递归就终止了呗。因此当链表只剩一个节点或者没有节点的时候，自然递归就终止了。

2. 找返回值。 我们希望向上一级递归返回什么信息？由于我们的目的是两两交换链表中相邻的节点，因此自然希望交换给上一级递归的是已经完成交换处理，即已经处理好的链表。

3. 本级递归应该做什么。 结合第二步，看下图！由于只考虑本级递归，所以这个链表在我们眼里其实也就三个节点：head、head.next、已处理完的链表部分。而本级递归的任务也就是交换这3个节点中的前两个节点，就很easy了。

lass Solution {
    public ListNode swapPairs(ListNode head) {
      //终止条件：链表只剩一个节点或者没节点了，没得交换了。返回的是已经处理好的链表
      if(head == null || head.next == null) return head;
      //一共三个节点:head, temp, swapPairs(temp.next)
      //下面的任务便是交换这3个节点中的前两个节点
      ListNode temp = head.next;
      Head.next = swapPairs(temp.next);
      //根据第二步：返回给上一级的是当前已经完成交换后，即处理好了的链表部分
      temp.next = head;

      return temp;
   }
}

平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3
   / 
  9  20
    /  
   15   7

返回 true 。

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        return Math.abs(deepth(root.left) - deepth(root.right)) < 2 && isBalanced(root.left) && isBalanced(root.right);
    }

    //树的深度
    public int deepth(TreeNode root) {
        if(root == null)  return 0;
        return Math.max(deepth(root.left), deepth(root.right)) + 1;       
    }

}