1 /*
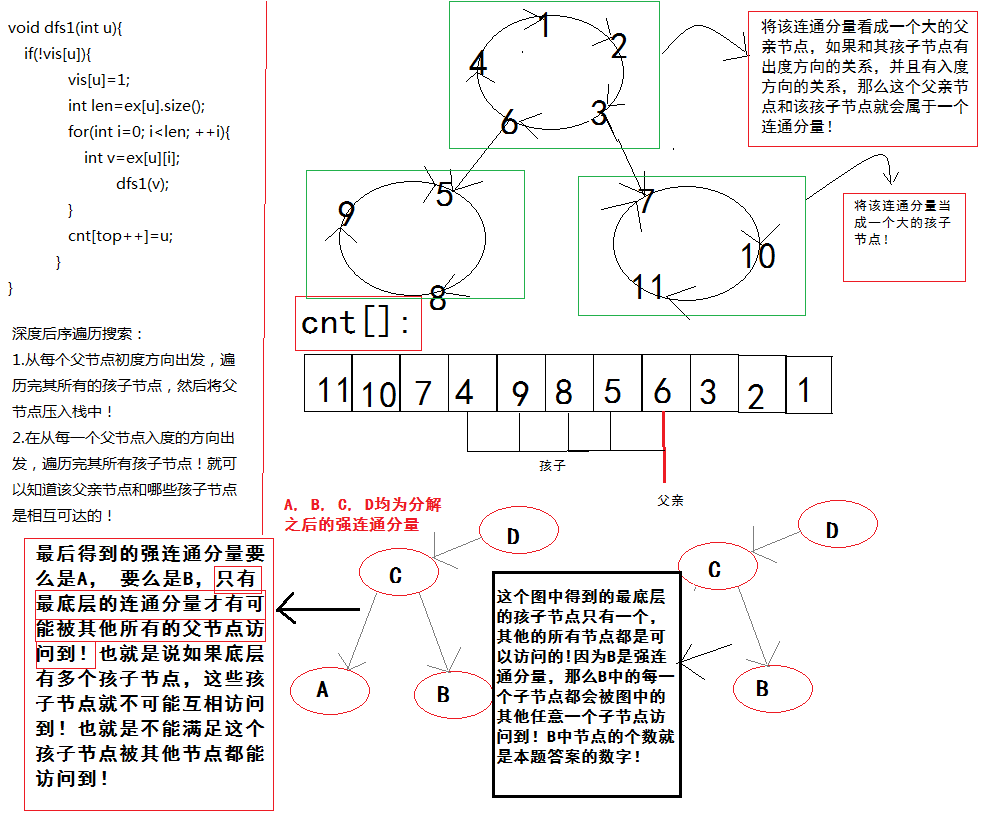
2 tarjan 算法果然nb! 首先我们利用该算法将所有的强连通分量分开!
3 然后将每一个连通分量看成是一个点,这样就成了一个有向无环图!
4 接着判断初度为 0 的点一共有多少个!如果只有一个,那么最终的答案就是
5 这个节点终所有子节点的个数!也就是说这个节点中的每一个子节点都能
6 其他的所有节点到达!
7
8 如果初度为 0 的点多余1个,那么对不起,不能满足某个节点恰好能被其他所有
9 的节点访问到!
10 */#include<iostream>
11 #include<cstdio>
12 #include<vector>
13 #include<stack>
14 #include<cstring>
15 #define M 10005
16 using namespace std;
17
18 vector<int>edge[M];
19 stack<int>s;
20 int low[M], vis[M];
21 int sccN[M], pre[M];
22 int n, m;
23 int dfs_clock, cnt;
24
25 void dfs(int u){//tarjan 算法
26 int len = edge[u].size();
27 pre[u]=low[u]=++dfs_clock;
28 s.push(u);
29 for(int i=0; i<len; ++i){
30 int v=edge[u][i];
31 if(!pre[v]){
32 dfs(v);
33 low[u]=min(low[u], low[v]);
34 }
35 else if(!sccN[v])
36 low[u] = min(low[u], pre[v]);
37 }
38 if(low[u]==pre[u]){
39 ++cnt;
40 while(1){
41 int v=s.top();
42 s.pop();
43 sccN[v]=cnt;
44 if(u==v) break;
45 }
46 }
47 }
48
49 int main(){
50 while(scanf("%d%d", &n, &m)!=EOF){
51 dfs_clock=cnt=0;
52 memset(pre, 0, sizeof(pre));
53 memset(sccN, 0, sizeof(sccN));
54 memset(vis, 0, sizeof(vis));
55 while(m--){
56 int u, v;
57 scanf("%d%d", &u, &v);
58 edge[u].push_back(v);
59 }
60 for(int i=1; i<=n; ++i)
61 if(!pre[i])
62 dfs(i);
63 int num=0;
64 for(int i=1; i<=n; ++i)
65 if(sccN[i]==1)
66 ++num;
67 int count=0;
68 memset(vis, 0, sizeof(vis));
69 for(int i=1; i<=n; ++i){
70 int len=edge[i].size();
71 for(int j=0; j<len; ++j)
72 if(sccN[i] != sccN[edge[i][j]]){
73 vis[sccN[i]]=1;
74 break;
75 }
76 }
77
78 for(int i=1; i<=cnt; ++i)
79 if(!vis[i]) ++count;
80 if(count==1)
81 printf("%d
", num);
82 else printf("0
");
83 for(int i=1; i<=n; ++i)
84 edge[i].clear();
85 while(!s.empty())
86 s.pop();
87 }
88 return 0;
89 }
1 /*比较慢的方法就是:利用tarjan算法将所有的强连通分量进行分离之后,
2 将每一个强连通分量看成是一个点,如果有满足我们答案的解,那么初度为零
3 点一定只有一个,并且这个点的所有子节点的编号是 1!那么我们先计算出子节点
4 编号为 1的个数, 然后在判断其他的强连通分量的节点是否能够到达编号为 1 的
5 强连通分量! */
6 #include<iostream>
7 #include<cstdio>
8 #include<vector>
9 #include<stack>
10 #include<cstring>
11 #define M 10005
12 using namespace std;
13
14 vector<int>edge[M];
15 stack<int>s;
16 int low[M], vis[M], used[M];
17 int sccN[M], pre[M];
18 int n, m;
19 int dfs_clock, cnt, sum, xx;
20
21 void dfs(int u){
22 int len = edge[u].size();
23 pre[u]=low[u]=++dfs_clock;
24 s.push(u);
25 for(int i=0; i<len; ++i){
26 int v=edge[u][i];
27 if(!pre[v]){
28 dfs(v);
29 low[u]=min(low[u], low[v]);
30 }
31 else if(!sccN[v])
32 low[u] = min(low[u], pre[v]);
33 }
34 if(low[u]==pre[u]){
35 ++cnt;
36 while(1){
37 int v=s.top();
38 s.pop();
39 sccN[v]=cnt;
40 if(u==v) break;
41 }
42 }
43 }
44
45 int dfs2(int u){
46 int len=edge[u].size();
47 if(sccN[u]==1){//到达之后就不在进行任何搜索
48 sum+=xx;
49 return 1;
50 }
51 vis[u]=1;
52 for(int i=0; i<len; ++i){
53 int v=edge[u][i];
54 if(!vis[v]){
55 if(dfs2(v))
56 return 1;
57 }
58 }
59 return 0;
60 }
61
62 int main(){
63 while(scanf("%d%d", &n, &m)!=EOF){
64 dfs_clock=cnt=0;
65 memset(pre, 0, sizeof(pre));
66 memset(sccN, 0, sizeof(sccN));
67 memset(vis, 0, sizeof(vis));
68 memset(used, 0, sizeof(used));
69 while(m--){
70 int u, v;
71 scanf("%d%d", &u, &v);
72 edge[u].push_back(v);
73 }
74 for(int i=1; i<=n; ++i)
75 if(!pre[i])
76 dfs(i);
77 int num=0;
78 sum=0;
79 used[1]=1;
80 for(int i=1; i<=n; ++i){
81
82 if(sccN[i]==1)
83 ++num;
84 else if(!used[sccN[i]]){
85 memset(vis, 0, sizeof(vis));
86 xx=sccN[i];
87 used[sccN[i]]=1;
88 dfs2(i);
89 }
90 }
91
92 if(sum==(cnt+1)*cnt/2-1)//最后将能到达标号为1的连通分量的所有强连通分量的标号加起来
93 printf("%d
", num);
94 else printf("0
");
95 for(int i=1; i<=n; ++i)
96 edge[i].clear();
97 while(!s.empty())
98 s.pop();
99 }
100 return 0;
101 }