概念
首先是最近公共祖先的概念(什么是最近公共祖先?):
在一棵没有环的树上,每个节点肯定有其父亲节点和祖先节点,而最近公共祖先,就是两个节点在这棵树上深度最大的公共的祖先节点。
换句话说,就是两个点在这棵树上距离最近的公共祖先节点。
所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。
有人可能会问:那他本身或者其父亲节点是否可以作为祖先节点呢?
答案是肯定的,很简单,按照人的亲戚观念来说,你的父亲也是你的祖先,而LCA还可以将自己视为祖先节点。
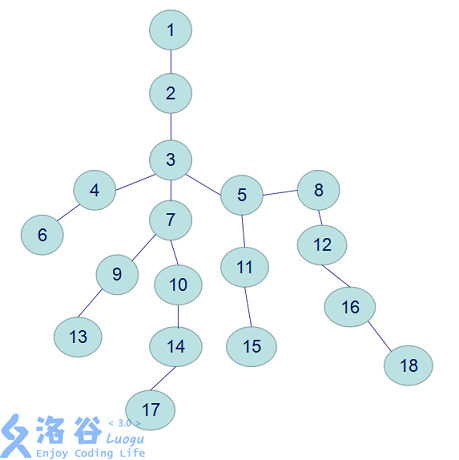
举个例子吧,如下图所示4和5的最近公共祖先是2,5和3的最近公共祖先是1,2和1的最近公共祖先是1。
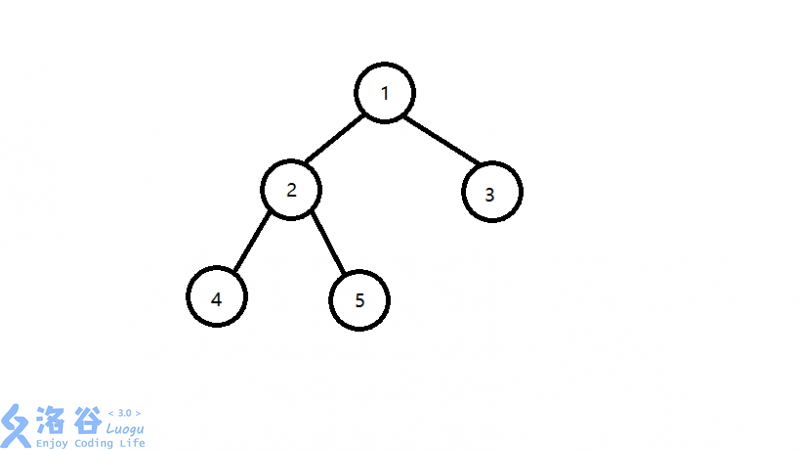
这就是最近公共祖先的基本概念了,那么我们该如何去求这个最近公共祖先呢?
通常初学者都会想到最简单粗暴的一个办法:对于每个询问,遍历所有的点,时间复杂度为(O(n*q)) ,很明显,(n)和(q)一般不会很小。
怎么办办?
LCA其实有很多种解法,这里介绍几个
一、Tarjan大法好!
什么是(Tarjan)(离线)算法呢?顾名思义,就是在一次遍历中把所有询问一次性解决,所以其时间复杂度是(O(n+q))。
(Tarjan)算法的优点在于相对稳定,时间复杂度也比较居中,也很容易理解。
下面详细介绍一下(Tarjan)算法的基本思路:
-
任选一个点为根节点,从根节点开始。
-
遍历该点(u)所有子节点(v),并标记这些子节点(v)已被访问过。
-
若是(v)还有子节点,返回(2),否则下一步。
-
合并(v)到(u)上。
-
寻找与当前点(u)有询问关系的点(v)。
-
若是(v)已经被访问过了,则可以确认(u)和(v)的最近公共祖先为(v)被合并到的父亲节点(a)。
遍历的话需要用到(dfs)来遍历(相信来看的人都懂吧...),至于合并,最优化的方式就是利用并查集来合并两个节点。
- 伪代码
Tarjan(u)//marge和find为并查集合并函数和查找函数
{
for each(u,v) //访问所有u子节点v
{
Tarjan(v); //继续往下遍历
marge(u,v); //合并v到u上
标记v被访问过;
}
for each(u,e) //访问所有和u有询问关系的e
{
如果e被访问过;
u,e的最近公共祖先为find(e);
}
}
个人感觉这样还是有很多人不太理解,所以打算模拟一遍给大家看。
假设我们有一组数据 9个节点 8条边 联通情况如下:
1--2,1--3,2--4,2--5,3--6,5--7,5--8,7--9 即下图所示的树
设我们要查找最近公共祖先的点为9--8,4--6,7--5,5--3;
设f[]数组为并查集的父亲节点数组,初始化f[i]=i,vis[]数组为是否访问过的数组,初始为0;
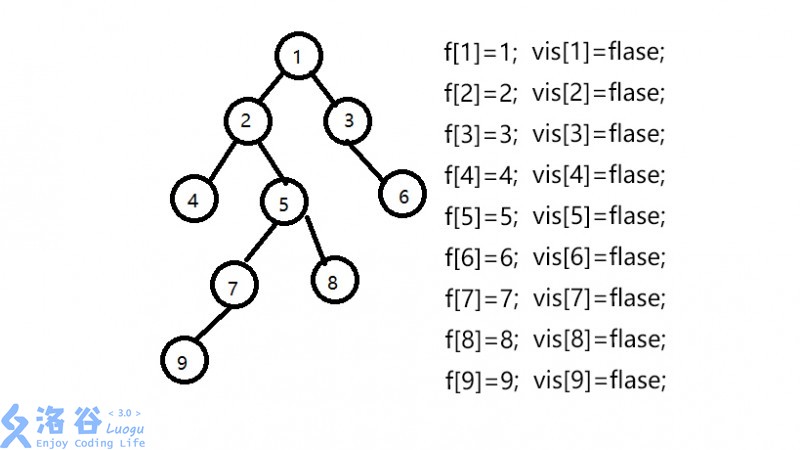
下面开始模拟过程:
取1为根节点,往下搜索发现有两个儿子2和3;
先搜2,发现2有两个儿子4和5,先搜索4,发现4没有子节点,则寻找与其有关系的点;
发现6与4有关系,但是vis[6]=0,即6还没被搜过,所以不操作;
发现没有和4有询问关系的点了,返回此前一次搜索,更新vis[4]=1;
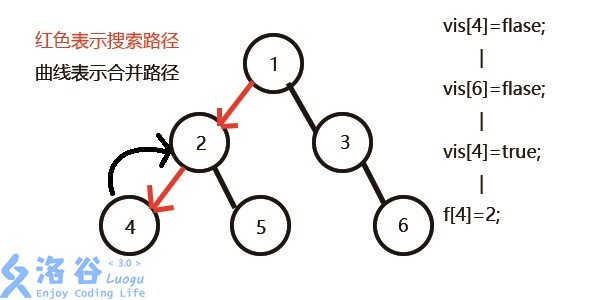
表示4已经被搜完,更新f[4]=2,继续搜5,发现5有两个儿子7和8;
先搜7,发现7有一个子节点9,搜索9,发现没有子节点,寻找与其有关系的点;
发现8和9有关系,但是vis[8]=0,即8没被搜到过,所以不操作;
发现没有和9有询问关系的点了,返回此前一次搜索,更新vis[9]=1;
表示9已经被搜完,更新f[9]=7,发现7没有没被搜过的子节点了,寻找与其有关系的点;
发现5和7有关系,但是vis[5]=0,所以不操作;
发现没有和7有关系的点了,返回此前一次搜索,更新vis[7]=1;
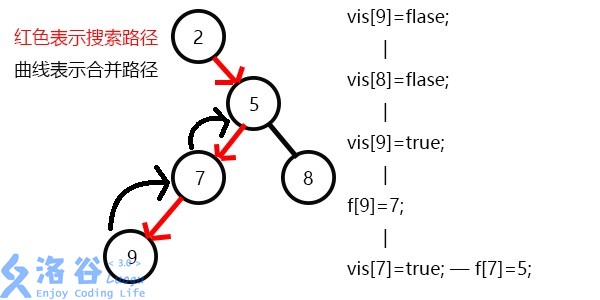
表示7已经被搜完,更新f[7]=5,继续搜8,发现8没有子节点,则寻找与其有关系的点;
发现9与8有关系,此时vis[9]=1,则他们的最近公共祖先为find(9)=5;
(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)
发现没有与8有关系的点了,返回此前一次搜索,更新vis[8]=1;
表示8已经被搜完,更新f[8]=5,发现5没有没搜过的子节点了,寻找与其有关系的点;
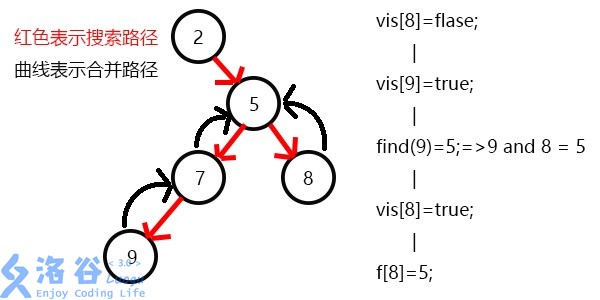
发现7和5有关系,此时vis[7]=1,所以他们的最近公共祖先为find(7)=5;
(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)
又发现5和3有关系,但是vis[3]=0,所以不操作,此时5的子节点全部搜完了;
返回此前一次搜索,更新vis[5]=1,表示5已经被搜完,更新f[5]=2;
发现2没有未被搜完的子节点,寻找与其有关系的点;
又发现没有和2有关系的点,则此前一次搜索,更新vis[2]=1;
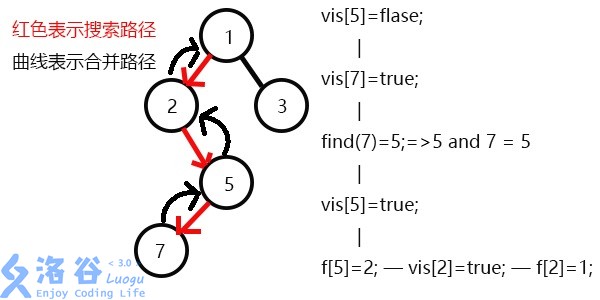
表示2已经被搜完,更新f[2]=1,继续搜3,发现3有一个子节点6;
搜索6,发现6没有子节点,则寻找与6有关系的点,发现4和6有关系;
此时vis[4]=1,所以它们的最近公共祖先为find(4)=1;
(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)
发现没有与6有关系的点了,返回此前一次搜索,更新vis[6]=1,表示6已经被搜完了;
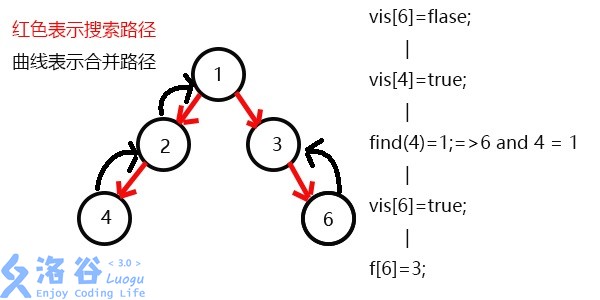
更新f[6]=3,发现3没有没被搜过的子节点了,则寻找与3有关系的点;
发现5和3有关系,此时vis[5]=1,则它们的最近公共祖先为find(5)=1;
(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)
发现没有和3有关系的点了,返回此前一次搜索,更新vis[3]=;
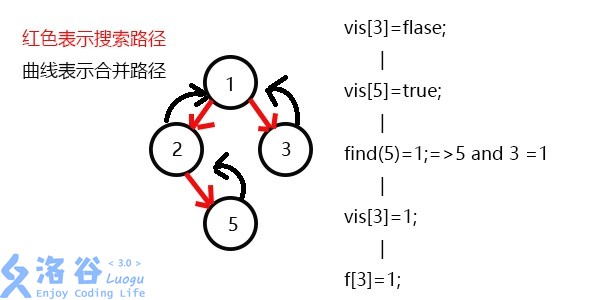
更新f[3]=1,发现1没有被搜过的子节点也没有有关系的点,此时可以退出整个dfs了。
经过这次dfs我们得出了所有的答案,有没有觉得很神奇呢?是否对Tarjan算法有更深层次的理解了呢?
二、倍增LCA
何为倍增?
所谓倍增,就是按(2)的倍数来增大,也就是跳 (1,2,4,8,16,32……) 不过在这我们不是按从小到大跳,而是从大向小跳,即按(……32,16,8,4,2,1)来跳,如果大的跳不过去,再把它调小。这是因为从小开始跳,可能会出现“悔棋”的现象。拿 55 为例,从小向大跳,(5≠1+2+4),所以我们还要回溯一步,然后才能得出(5=1+4);而从大向小跳,直接可以得出(5=4+1)。这也可以拿二进制为例,(5(101)),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
这里以编号为17和18结点为例
(17->3)
(18->5->3)
可以看出向上跳的次数大大减小。这个算法的时间复杂度为(O(nlogn)),已经可以满足大部分的需求。
想要实现这个算法,首先我们要记录各个点的深度和他们(2^i)级的的祖先,用数组( m{deep})表示每个节点的深度,(fa[i][j])表示节点(i)的(2^j)级祖先。 代码如下:
inline void getdeep(int now,int father)//now表示当前节点,father表示它的父亲节点
{
deep[now]=deep[father]+1;
fa[now][0]=father;
for(int i=1;(1<<i)<=deep[now];i++)
fa[now][i]=fa[fa[now][i-1]][i-1];//这个转移可以说是算法的核心之一
//意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先
//2^i=2^(i-1)+2^(i-1)
for(int i=head[now];i;i=edge[i].next)//注意:尽量用链式前向星来存边,速度会大大提升
{
if(edge[i].to==father)continue;
getdeep(edge[i].to,now);
}
}
然后我们要算出log2n
log2n=log(n)/log(2)+0.5;
接下来就是倍增LCA了,我们先把两个点提到同一高度,再统一开始跳。
但我们在跳的时候不能直接跳到它们的LCA,因为这可能会误判,比如(4)和(8),在跳的时候,我们可能会认为(1)是它们的LCA,但(1)只是它们的祖先,它们的LCA其实是(3)。所以我们要跳到它们LCA的下面一层,比如(4)和(8),我们就跳到(4)和(5),然后输出它们的父节点,这样就不会误判了。
inline int lca(int u,int v)
{
int deepu=deep[u],deepv=deep[v];
if(deepu!=deepv)//先跳到同一深度
{
if(deep[u]<deep[v])
{
swap(u,v);
swap(deepu,deepv);
}
int d=deepu-deepv;
for(int i=0;i<=log2n;i++)
if((1<<i)&d)u=fa[u][i];
}
if(u==v)return u;
for(int i=log2n;i>=0;i--)
{
if(deep[fa[u][i]]<=0)continue;
if(fa[u][i]==fa[v][i])continue;
else u=fa[u][i],v=fa[v][i];//因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。
}
return fa[u][0];
}
完整的求17和18的LCA的路径:
(17->10->7->3)
(18->16->8->5->3)
解释:首先,(18)要跳到和(17)深度相同,然后(18)和(17)一起向上跳,一直跳到LCA的下一层((17)是(7),(18)是(5)),此时LCA就是它们的父亲
总体来说就是这样了;