程序设计思路:
求一个二维数组中的最大联通子数组,第一步需要做的就是将一个二位数组转化成图的形式,根据题目的要求可以,每一行每一列的相互紧邻的元素都是联通的,而处于对角线位置的运算则不是相互联通的,另外,前一行的最后一个元素与下一行的第一个元素也不是联通的。为表示数组元素之间的关联程度采用一个二位数组Relation来表示,若元素存在关联关系,则数组中存入1;后续的工作就是遍历,同样采用动态规划的思想去完成,只不过需要多次遍历。题目中要求从一个文件中读入数组的行数列数和元素,因此,在运算之前要写一个函数从文件中读入,暂存到数组和变量中。
程序源代码:
//返回一个二维整数数组中最大联通子数组的和 //2016-04-01 #include<iostream> #include<fstream> using namespace std; //从文件中读取数组到内存中 void ReanformFile(int &row, int &col, int E[]) { ifstream infile; infile.open("input.txt", ios::in | ios::_Nocreate); //打开当前目录下的txt文档 if (!infile) { cerr << "open error!" << endl; } infile >> row >> col; for (int i = 1; i < (row*col + 1); i++) { infile >> E[i]; //将文件中的元素存放到一个一维数组中 } infile.close(); } //记录二维数组中每个元素与其他元素之间的联系,若相紧邻,则将二维数组中的元素值设置为1,处于对角线位置的元素没有关联关系 void outputElement(int row, int col, int E[], int R[][100]) { for (int i = 1; i <(row*col + 1); i = i + col) { for (int j = i; j <= i + col - 2; j++) { R[j][j + 1] = 1; R[j + 1][j] = 1; } } for (int i = 1 + col; i<(row*col); i = i + col) { for (int j = i; j <= i + row - 1; j++) { R[j][j - col] = 1; R[j - col][j] = 1; } } //以二位数组的形式输出文档中的元素值 for (int i = 1; i <= (row*col); i++) { cout << E[i]; if (R[i][i + 1] == 1) cout << " "; else cout << endl; } } //查找某个元素周围的元素是否可以加入到最大联通子数组中 void Select(int row, int col, int E[], int R[][100], int v, int visit[], int &max, int &temp) { visit[v] = 1; max = max + E[v]; if (max >= temp) { temp = max; } int m = 0, n = 0; for (int i = 1; i <= (row*col); i++) { for (int j = 1; j <= (row*col); j++) { if ((visit[i] == 0) && (R[j][i] == 1) && (visit[j] == 1)) { m = i; n = 1; break; } } if (n == 1) break; } for (int i = 1; i <= (row*col); i++) //查找是否存在比该元素更大的元素 { for (int j = 1; j <= (row*col); j++) { if ((visit[i] == 0) && (R[j][i] == 1) && (visit[j] == 1)) { if (E[m] < E[i]) { m = i; } } } } if (temp + E[m] < 0) { R[v][m] = 0; } else Select(row, col, E, R, m, visit, max, temp); } int main() { int row = 0, col = 0; //存储行数和列数 int Element[100]; //存储每个元素的值 int Relation[100][100]; int v = 1, temp[100] = { 0 }; ReanformFile(row, col, Element); outputElement(row, col, Element, Relation); for (int i = 1; i <= (row*col); i++) { if (Element[i]<0) { temp[i] = Element[i]; } else { int max = 0; int visit[100] = { 0 }; Select(row, col, Element, Relation, i, visit, max, temp[i]); } } int max = temp[1]; for (int i = 2; i <= (row*col); i++) { if (temp[i] > max) { max = temp[i]; } } cout << "最大子数组的和为:" << max << endl; return 0; }
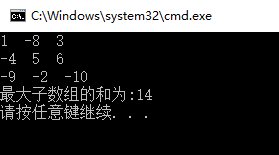
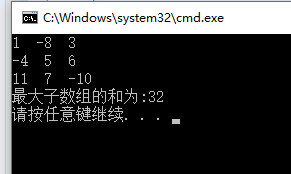
运行结果截图: