AVL(二叉平衡树) 的实现

一颗AVL树是其每个节点的左子树与右子树的高度最多差1的二叉查找树。

在插入过程中，利用旋转的办法保持这个性质。

共分四种情形：

1、  树T的左孩子的左子树上新插入节点导致破坏平衡性：

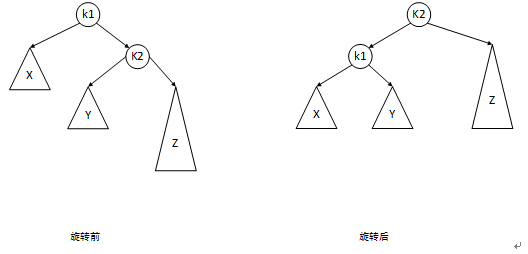
如下图左边所示，因为在子树X中新加入一个节点，导致k2处的平衡性被破坏

通过如右边所示的旋转，可以使得整棵树重新变得平衡。

2、 树T的右孩子的右子树上新插入节点导致破坏平衡性

这种情形跟上面那种情形是对称的。

3、树T的左孩子的右子树上新插入节点导致破坏平衡性

此时照搬情形1的旋转方法已经不能奏效了。

考虑将Y这部分散开来看：

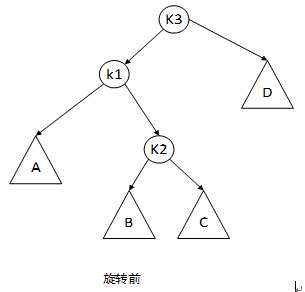
可经由两次旋转解决问题：

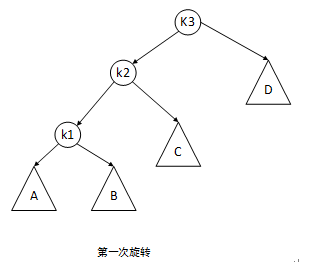
可以发现，经过第一次旋转之后，问题已经变成了情形1，可再进行一次单旋转解决：

4、树T的右孩子的左子树上新插入结点，这时与情形3完全对称，可类似解决。

以下是实现部分。

仅实现插入操作，删除一般是惰性的。还有一点假设相同元素不出现在树结构中。

avl.h

#pragma once
using Elemtype = int;
struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;

//AvlTree MakeEmpty(AvlTree T);
//Position Find(Elemtype X, AvlTree T);
//Position FindMin(AvlTree T);
//Position FindMax(AvlTree T);

AvlTree Insert(Elemtype X, AvlTree T);
//AvlTree Delete(Elemtype X, AvlTree T);

//Elemtype Retrieve(Position P);

 avl.cpp

#include "avl.h"
#include<cstdio>
#include<cstdlib>
#include<cassert>
#include<algorithm>
struct AvlNode{
	Elemtype Element;
	AvlTree Left;
	AvlTree Right;
	int Height;
};

static int Height(Position p){
	if (p == nullptr)
		return -1;
	else
		return p->Height;
}
static Position SingleRotateWithLeft(Position K2){
	Position K1;
	K1 = K2->Left;
	K2->Left = K1->Right;
	K1->Right = K2;

	K2->Height = std::max(Height(K2->Left), Height(K2->Right)) + 1;
	K1->Height = std::max(Height(K1->Left), Height(K1->Right)) + 1;

	return K1; /*New root*/
}
static Position SingleRotateWithRight(Position K2){
	Position K1;
	K1 = K2->Right;
	K2->Right = K1->Left;
	K1->Left = K2;

	K2->Height = std::max(Height(K2->Left), Height(K2->Right)) + 1;
	K1->Height = std::max(Height(K1->Left), Height(K1->Right)) + 1;

	return K1; /*New root*/
}
static Position DoubleRotateWithLeft(Position K3){
	K3->Left = SingleRotateWithRight(K3->Left);
	return SingleRotateWithLeft(K3);
}
static Position DoubleRotateWithRight(Position K3){
	K3->Right = SingleRotateWithLeft(K3->Right);
	return SingleRotateWithRight(K3);
}
AvlTree Insert(Elemtype X, AvlTree T){
	if (T == nullptr){
		/*Create and return a one-node tree*/
		T = (AvlTree)malloc(sizeof(struct AvlNode));
		assert(T != nullptr, "Out of Space");
		T->Element = X; T->Height = 0;
		T->Left = T->Right = nullptr;
	}
	else if (X < T->Element){
		T->Left = Insert(X, T->Left);
		if (Height(T->Left) - Height(T->Right) == 2){
			if (X < T->Left->Element){
				T = SingleRotateWithLeft(T);
			}
			else{
				T = DoubleRotateWithLeft(T);
			}
		}
	}
	else if (X > T->Element){
		T->Right = Insert(X, T->Right);
		if (Height(T->Right) - Height(T->Left) == 2){
			if (X > T->Right->Element){
				T = SingleRotateWithRight(T);
			}
			else{
				T = DoubleRotateWithRight(T);
			}
		}
	}
	/*Else X is in the tree already; we'll do nothing */
	T->Height = std::max(Height(T->Left), Height(T->Right)) + 1;
	return T;
}