看电影(movie)：组合数

Description

到了难得的假期，小白班上组织大家去看电影。但由于假期里看电影的人太多，很难做到让全班看上同一场电影，最后大家在一个偏僻的小胡同里找到了一家电影院。但这家电影院分配座位的方式很特殊，具体方式如下：

1. 电影院的座位共有K个，并被标号为1…K，每个人买完票后会被随机指定一个座位，具体来说是从1…K中等可能的随机选取一个正整数，设其为L。
2. 如果编号L的座位是空位，则这个座位就分配给此人，否则将L加一，继续前面的步骤。
3. 如果在第二步中不存在编号L的座位，则该人只能站着看电影，即所谓的站票。

小白班上共有N人（包括小白自己），作为数学爱好者，小白想知道全班都能够有座位的概率是多少。

 

Input

输入文件第一行有且只有一个正整数T，表示测试数据的组数。
第2～T+1行，每行两个正整数N,K，用单个空格隔开，其含义同题目描述。

Output

输出文件共包含T行。
第i行应包含两个用空格隔开的整数A,B，表示输入文件中的第i组数据的答案为A/B。（注意，这里要求将答案化为既约分数）

Sample Input

3
1 1
2 1
2 2

Sample Output

1 1
0 1
3 4

Hint

对于100%的数据 T<=50,N,K<=200​​,1<=n<=101810^{18}10​18​​,1<=q<=10510^510​5​​

先讲我的摸索出公式心路历程，再讲正常的方法啦，可以自行跳过

没有头绪，推不出式子，怎么办？

模小点打表啊（在机房的时间不够没来得及打代码来打表，所以上课手模超辛酸）

分母是显而易见的，kⁿ，找分子：

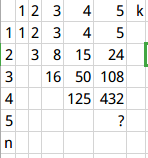4节文化课的成果，再大的点真的模不出来，包括那个5 5

先观察n=k的情况，可以发现是（n+1）^n-1

猜测问号处的值是6⁴=1296

第1行，逐项做差：1 1 1 1 1

第2行，也是：5 7 9。再来一次：2 2。

第3行，做差：34 58。再来：24。

发现，做差几次后，会得到常数列。做差的次数为n次。证明这序列是个n-1次函数。

再发现：通过观察右偏下45度的每一条对角线，f（n，k）一定会被（k-n+1）整除。整除之后的商都是次方数。

找到规律：分子是（k-n+1）×（k+1）^n-1

接下来考虑约分，显而易见分子上的(k+1)和分母的k不可约分，只有k-n+1需要与k约分

但是可能不止约了一次！如k=18而n=15，那么分别是4和18进行约分

剩下2和9，不要着急往分母分子上乘，因为我们可以拿出另一个k=18，把2约干净。

所以要不断除，直到k的个数不够或者gcd为1。

正常思路：

推出了式子之后，我开始考虑这个式子是什么含义：

我们增加一个座位，表示被干出去的人，最后只需检察这个位置上有没有人即可。

我们把所有作为连成一个环，计算合法方案数即可。

#include<cstdio>
struct gj{
    long long x[40];int ws;
     friend void operator*=(gj &a,int t){
         for(int i=0;i<=a.ws;++i)a.x[i]*=t;
         for(int i=0;i<=a.ws;++i)a.x[i+1]+=a.x[i]/1000000000000000,a.x[i]%=1000000000000000;
         if(a.x[a.ws+1])a.ws=a.ws+1;
     }
     void print(){
         printf("%lld",x[ws]);x[ws]=0;
         for(int i=ws-1;i>=0;--i)printf("%015lld",x[i]),x[i]=0;
         ws=0;x[0]=1;
     }
}fz,fm;
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int k,n,t;
int main(){
    scanf("%d",&t);fz.x[0]=fm.x[0]=1;
    while(t--){
        scanf("%d%d",&n,&k);
        if(n>k){puts("0 1");continue;}
        int ex=k-n+1,tms=n;
        while(gcd(ex,k)!=1&&tms)fm*=k/gcd(ex,k),ex/=gcd(ex,k),tms--;
        fz*=ex;
        for(int i=n-1;i;i--)fz*=k+1;
        for(int i=tms;i;--i)fm*=k;
        fz.print();putchar(' ');fm.print();puts("");
    }
}