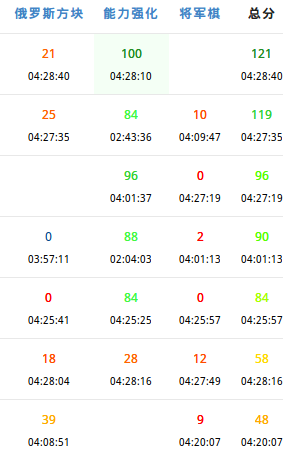

久违的运气啊。。。
电脑炸了,然后$T3$大提答文件太大提交框粘贴时没有粘上去,丢了$7$分。
只能说,这场考试饶有趣味,但是这些考试题是真的无聊。
上来一看,$T2$是个强化的原题,不会。
不会怎么行啊是要被$NC$骂的啊,划拉了个$T1$模拟就开始头铁$T2$。
其实大概也是看了一下三道题,$T1$模拟,正解大概是大数据结构而且不很好想,$T3$毒瘤提答估计也没人能拿到多少分。
所以说如果真的把$T2$头铁出来的话排名应该不会低。于是我就的确是这么做的。
原来指数型生成函数一道题没做过,$minmax$容斥只做过一道题的我又开始了现场发明的过程。
$8:20$开始弄,非常惊险,$11:35$最后终于调出来了。感觉整个人都不一样了。
最后$25$分钟大概卡了卡常(本机太慢了大样例都跑了好久所以特别慌)
六七分钟写个$dfs$去$T3$水分但是电脑卡没交上去。
然后结果得亏我$T2$卡常了,$5$个正解只有我卡进去了。。。
积攒了不知道多久的$RP$终于爆发了。(所以以后几场我是不是又有考炸的理由了?
改题真的不是我不改。。。这题让人看着就恶心。。。$T3$得写$10$个巨型数据结构,$T1$得写一个细节超级多的数据结构。。
最后去$T3$写了三份奇怪的东西拿下$3$个点,然后又优化了半天$dfs$最后拿到了一个奇妙的$38$分结束这一天。
T1:俄罗斯方块
大意:若干种四联通块,按照俄罗斯方块规则下落,(不消除),求每次下落之后的全场最大高度值。注意,四联通快大小可能远大于$4$。$n,size le 10^5$
可以发现,每次块下落的时候它的高度只与它所在区间出现的所有块有关。
于是每次用到时处理两个块之间的关系,并记忆化下来。
同样的,小块的跑暴力来保证常数。
用一个$set$像$ODT$一样维护区间信息。均摊复杂度对。
具体的操作是,从大到小枚举可行的高度,然后把两个位置是否有块的信息进行按位与,如果与出来是$1$就说明撞上了,手写$bitset$。
思路粗暴(虽然我也没想到)代码恶心。这题就咕掉了。
T2:能力强化
大意:你有$n$种喂玉米的方式,每种是喂$a_i$粒。有$m$只鸽子,吃$k$粒之后会饱。随机选一种方式随机喂一只鸽子。期望几次后全吃饱。$n,k,m le 100$
$n$为啥不出到$10^7?$
全吃饱不好求,于是我们转而去求有且只有一只吃饱。这是典型的$minmax$容斥。
$minmax$之后发现集合还是有点多,然而鸽子之间没有区别,所以你只在意集合大小,最后乘组合数就好了。
设$p_i$表示对一只鸽子投食$i$次恰好在第$i$次的时候饱了的概率。这个可以直接背包$dp$或者$OGF$弄出来。时间复杂度$O(k^3)或$O(nk^2)$或$O(k^2logk)$
设$q_i$表示喂了一只鸽子$q$次它还没饱的概率,那么$q_i =1 - sumlimits_{j=0}^{i} p_j$
对这俩玩意分别搞生成函数,那么最后$min(i)$的答案就与$PQ^{i-1}$有关。
发现玉米扔的顺序计做不同方案,所以要考虑排列,喂给一只鸽子的玉米的内部顺序在$p,q$中已经分别考虑到了,所以剩下的是多重集排列。
于是果断采用指数型生成函数。
但是不对劲,发现我们已经知道了最后一粒玉米一定在最后一只鸽子嘴里,所以不参与排列,于是下标要整体平移一位。
期望等于概率乘原值。但是因为你统计了方案数,所以最后还要除掉总方案书$m^i$这样才是真概率。
概率求出之后,原值是多少?$j+1$(因为平移了)。但还是不对。因为$minmax$中并不能偷换概念。
所以详细的说来$min(i)$是指往所有的$m$只鸽子里丢玉米然后其中的$i$只中最早饱的一只的期望时间。
然而按照你刚才求出来的那个东西是只往$i$只鸽子里扔的,所以最后原值也要乘$frac{m}{i}$
然后就没了。就是常数问题了。
我觉得因为数据范围比较小所以暴力卷及不会比$NTT$慢太多于是就暴力卷了。
(卷积的形式大概是$O(k^2) * O(k)$的,我感觉把那个$O(k)$的转成$O(k^2)$的做$NTT$怪浪费的)
然后取模优化,善待擦车,$m^i$递推而非快速幂。问题就不大了吧。
时间复杂度是小常数$O(n^4)$或大常数$O(n^3logn)$。$n,m,k$同级别不区分。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mod 998244353 4 #define S 22222 5 int n,m,k,res[S],r[S],p0[S],fac[S],inv[S],finv[S],P[S],Q[S],Ans; 6 int mo(int x){return x>=mod?x-mod:x;} 7 int main(){ 8 cin>>n>>m>>k; 9 fac[0]=fac[1]=inv[1]=finv[1]=finv[0]=1; 10 for(int i=2;i<=20000;++i)fac[i]=fac[i-1]*1ll*i%mod,inv[i]=mod-mod/i*1ll*inv[mod%i]%mod,finv[i]=finv[i-1]*1ll*inv[i]%mod; 11 for(int i=1,x;i<=n;++i)cin>>x,p0[x]=mo(p0[x]+inv[n]); 12 res[0]=Q[0]=1; 13 for(int t=0;t<k;++t){ 14 for(int i=0;i<k;++i)if(res[i])for(int j=0;j<=k;++j)r[i+j]=(r[i+j]+1ll*res[i]*p0[j])%mod; 15 for(int i=0;i<k;++i)res[i]=r[i],r[i]=0; 16 for(int i=k;i<k<<1;++i)P[t]=mo(P[t]+r[i]),r[i]=0; 17 Q[t+1]=mo(Q[t]-P[t]+mod); 18 } 19 int w=k-1; 20 for(int i=0;i<=k;++i)P[i]=1ll*P[i]*finv[i]%mod,Q[i]=1ll*Q[i]*finv[i]%mod; 21 for(int t=1,C;t<=m;++t){ 22 C=1ll*fac[m]*finv[t]%mod*finv[m-t]%mod; 23 for(int i=0,iv=1;i<=w;++i)Ans=(Ans + (t&1?1ll:mod-1ll) *C%mod* P[i]%mod*fac[i]%mod *(i+1)%mod* inv[t]%mod*m%mod*iv)%mod,iv=1ll*iv*inv[t]%mod; 24 for(int i=0;i<=w;++i)if(P[i])for(int j=0;j<k;++j)r[i+j]=(r[i+j]+1ll*P[i]*Q[j])%mod; 25 w+=k-1; 26 for(int i=0;i<=w;++i)P[i]=r[i],r[i]=0; 27 }cout<<Ans<<endl; 28 }
T3:将军棋
大意:提答,棋盘,每个格子有兵或障碍或空地。每次可以选定一个位置上的除了其中的1个以外的剩下所有兵走到相邻非空格子上,限定步操作后让尽量多格子上有兵,输出方案。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int x,y,stp,a[10000][10000],n,m; 4 void mov(int sx,int sy,int tx,int ty){} 5 void U(){cout<<x<<' '<<y<<' '<<'U'<<endl;x--;stp--;} 6 void D(){cout<<x<<' '<<y<<' '<<'D'<<endl;x++;stp--;} 7 void L(){cout<<x<<' '<<y<<' '<<'L'<<endl;y--;stp--;} 8 void R(){cout<<x<<' '<<y<<' '<<'R'<<endl;y++;stp--;} 9 void work(int d){if(!d)R();else if(d==1)L();else if(d==2)D();else U();} 10 const int dx[]={0,0,1,-1},dy[]={1,-1,0,0}; 11 int d[555][555]; 12 int dfs2_1(int tx,int ty,int fd){ 13 int mx=0;d[tx][ty]=-1; 14 for(int i=0;i<4;++i)if(i!=(fd^1)&&a[tx+dx[i]][ty+dy[i]]!=-1){ 15 int dep=dfs2_1(tx+dx[i],ty+dy[i],i); 16 if(dep>mx)mx=dep,d[tx][ty]=i; 17 }return mx+1; 18 } 19 void dfs2_2(int fd,int op=1){int q=d[x][y];//cerr<<x<<' '<<y<<' '<<fd<<' '<<stp<<endl; 20 for(int i=0;i<4;++i)if(stp>=2&&i!=(fd^1)&&(!op||i!=q)&&a[x+dx[i]][y+dy[i]]!=-1)stp--,work(i),dfs2_2(i,0),work(i^1),stp++; 21 if(d[x][y]!=-1&&op)stp++,work(q),dfs2_2(q); 22 } 23 int main(){ 24 /*freopen("generals1.out","w",stdout); 25 x=21;y=34;n=55;m=89; 26 for(int i=16;~i;--i){ 27 for(int j=20;j;--j)U(); 28 L(); 29 for(int j=20;j;--j)D(); 30 if(i)L(); 31 }D(); 32 33 int alx=x,aly=34;cerr<<x<<' '<<y<<' '<<alx<<' '<<aly<<' '<<stp<<endl; 34 while(alx+2<55){ 35 aly++; 36 while(y!=aly)R(); 37 while(x!=1)U(); 38 R();alx++;aly++; 39 while(x!=alx)D(); 40 while(y!=1)L(); 41 D();alx++; 42 } 43 aly++; 44 while(y!=aly)R(); 45 while(x!=1)U(); 46 while(aly+2<m){ 47 R();aly++; 48 while(x!=alx)D(); 49 R();aly++; 50 while(x!=1)U(); 51 } 52 R();R();D();D(); 53 int op=0; 54 while(x!=n){ 55 if(op)R();else L();D();op^=1; 56 } 57 while(y!=1)L();cerr<<-stp<<endl;*/ 58 59 freopen("generals2.out","w",stdout); 60 freopen("generals2.in","r",stdin); 61 cin>>n>>m>>stp; 62 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)cin>>a[i][j]; 63 for(int i=1;i<=n;++i)a[i][0]=a[i][m+1]=-1; 64 for(int i=1;i<=m;++i)a[0][i]=a[m+1][i]=-1; 65 stp-=dfs2_1(1,1,5)-1;cerr<<stp<<endl; 66 x=1;y=1;dfs2_2(5); 67 } 68 69 /*#include<bits/stdc++.h> 70 using namespace std; 71 int x,y,stp,a[10000][10000],n,m; 72 void mov(int sx,int sy,int tx,int ty){a[tx][ty]+=a[sx][sy]-1;a[sx][sy]=1;} 73 void up(){cout<<x<<' '<<y<<' '<<'U'<<endl;mov(x,y,x-1,y);x--;stp--;} 74 void down(){cout<<x<<' '<<y<<' '<<'D'<<endl;mov(x,y,x+1,y);x++;stp--;} 75 void left(){cout<<x<<' '<<y<<' '<<'L'<<endl;mov(x,y,x,y-1);y--;stp--;} 76 void right(){cout<<x<<' '<<y<<' '<<'R'<<endl;mov(x,y,x,y+1);y++;stp--;} 77 int o[4]={0,1,2,3};const int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; 78 void work(int o){if(!o)down();else if(o==1)up();else if(o==2)right();else left();} 79 void dfs(int op){ 80 if(!stp||a[x][y]==1)return; 81 random_shuffle(o,o+4); 82 for(int i=0;i<4;++i)if(a[x+dx[o[i]]][y+dy[o[i]]]==0){work(o[i]),dfs(op);return;} 83 if(op)return; 84 for(int i=0;i<4;++i)if(a[x+dx[o[i]]][y+dy[o[i]]]>=0){work(o[i]);return;} 85 } 86 int main(){ 87 freopen("generals10.out","w",stdout); 88 freopen("generals10.in","r",stdin); 89 cin>>n>>m>>stp;cout<<stp<<endl;cerr<<n<<' '<<m<<endl; 90 for(int i=1;i<=n;++i)a[i][0]=a[i][m+1]=-1; 91 for(int i=1;i<=m;++i)a[0][i]=a[n+1][i]=-1; 92 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&a[i][j]); 93 rbg: 94 int rstp=stp+1; 95 while(stp&&stp!=rstp){rstp=stp;for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(a[i][j]>1)x=i,y=j,dfs(1);} 96 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(a[i][j]>1){x=i,y=j,dfs(0);} 97 if(stp&&stp!=rstp)goto rbg;puts("???"); 98 while(stp)for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(a[i][j]>0)x=i,y=j,dfs(0); 99 }*/
其中还需要人脑模拟$test6$。

1 20 2 26 25 R 3 26 26 R 4 26 27 U 5 25 27 U 6 24 27 L 7 24 26 U 8 23 26 U 9 22 26 U 10 21 26 U 11 20 26 U 12 19 26 U 13 23 30 R 14 24 30 R 15 24 31 R 16 24 32 D 17 29 28 R 18 29 29 D 19 30 29 D 20 27 22 L 21 27 21 L
大概记一下有用的思路。
- 矩阵提答题一定要写个代码让它对其不然根本看不出性质。
- 注意找树。
- 多点汇聚用斯坦那树。
- 宽度不大用插头$dp$或者所谓的联通性$dp$。
- 树上两点的题可以考虑切断一条树边然后接着做。
- 随机数据可采用估价函数与贪心。
