将递归函数非递归化的一般方法(cont)

本文通过模拟汇编里的stack机制，构建一个自己的stack，然后将上一篇blog末尾的递归函数void bst_walk(bst_node_t *root)非递归化。

o libstack.h

#ifndef _LIBSTACK_H
#define _LIBSTACK_H

#ifdef    __cplusplus
extern "C" {
#endif

typedef void * uintptr_t; /* generic pointer to any struct */

uintptr_t *stack_init(size_t size);
void stack_fini();
int stack_isFull();
int stack_isEmpty();
void push(uintptr_t e);
void pop(uintptr_t *e);

#ifdef    __cplusplus
}
#endif

#endif /* _LIBSTACK_H */

o libstack.c

#include <stdio.h>
#include <stdlib.h>
#include "libstack.h"

/**
 * Basic Stack OPs are supported, including:
 *
 * 1. Construct/Destruct a stack
 * 2. Tell stack is full or empty
 * 3. push() and pop()
 *
 * == DESIGN NOTES ==
 *
 * There are 3 static variables reserved,
 *
 *     ss: stack segment
 *     sp: stack pointer
 *     sz: stack size
 *
 * And the stack looks like:
 *
 *               | RED | ss[-1]  ; SHOULD NEVER BE ACCESSED
 *     low-addr  +-----+ <------------TopOfStack-----------
 *        ^      |     | ss[0]
 *        |      |     | ss[1]
 *        |      | ... |
 *        |      |     |
 *        |      |     | ss[sz-1]
 *        |      +-----+ <------------BottomOfStack--------
 *     high-addr | RED | ss[sz]  ; SHOULD NEVER BE ACCESSED
 *
 * (1) If (sp - ss) == 0,  stack is full
 * (2) If (sp - ss) == sz, stack is empty
 * (3) Push(E): { sp -= 1;   *sp = E; }
 * (4) Pop(&E): { *E  = *sp; sp += 1; }
 */

static uintptr_t *ss = NULL; /* stack segment */
static uintptr_t *sp = NULL; /* stack pointer */
static size_t sz = 0;        /* stack size */

int stack_isFull()  { return (sp == ss); }
int stack_isEmpty() { return (sp == ss + sz); }

uintptr_t *
stack_init(size_t size)
{
    ss = (uintptr_t *)malloc(sizeof (uintptr_t) * size);
    if (ss == NULL) {
        fprintf(stderr, "failed to malloc
");
        return NULL;
    }

    sz = size;
    sp = ss + size;
    return ss;
}

void
stack_fini()
{
    free(ss);
}

void
push(uintptr_t e)
{
    sp -= 1;
    *sp = e;
}

void
pop(uintptr_t *e)
{
    *e = *sp;
    sp += 1;
}

1. 一旦栈被初始化后，栈指针sp一定是指向栈底，*sp不可访问（尤其是写操作），因为不在分配的内存有效范围内；

2. 对于入栈操作(push), 第一步是将sp-=1, 第二步是写入要入栈的元素 (*sp = E); (因为初始化后*sp的内存不可写，所以push操作一定率先改写sp)

3. 对于出栈操作(pop), 顺序与push相反，第一步取出sp指向的内存地址里的内容(E = *sp), 第二步才是将sp+=1;

o foo.c (简单测试)

/**
 * A simple test against stack OPs, including:
 * o stack_init(),   stack_fini()
 * o stack_isFull(), stack_isEmpty()
 * o push(), pop()
 */

#include <stdio.h>
#include "libstack.h"

static void
dump_stack(uintptr_t *ss, size_t size)
{
    (void) printf("%p: ", ss);
    for (int i = 0; i < size; i++) {
        if (ss[i] != NULL)
            (void) printf("%-10p ", *(ss+i));
        else
            (void) printf("0x%-8x ", 0x0);
    }
    printf("
");
}

int
main(int argc, char *argv[])
{
    size_t size = 4;

    uintptr_t *ss = stack_init(size);
    dump_stack(ss, size);

    for (int i = 0; !stack_isFull(); i++) {
        push((uintptr_t)(ss+i));
        dump_stack(ss, size);
    }

    (void) printf("
");

    uintptr_t e = NULL;
    for (; !stack_isEmpty();) {
        pop(&e);
        (void) printf(" (pop) got %-10p
", e);
    }

    stack_fini();

    return 0;
}

o Makefile

CC      = gcc
CFLAGS  = -g -Wall -std=gnu99 -m32
INCS    =

TARGET  = foo

all: ${TARGET}

foo: foo.o libstack.o
    ${CC} ${CFLAGS} -o $@ $^

foo.o: foo.c
    ${CC} ${CFLAGS} -c $< ${INCS}

libstack.o: libstack.c libstack.h
    ${CC} ${CFLAGS} -c $<

clean:
    rm -f *.o
clobber: clean
    rm -f ${TARGET}

o 编译和运行测试

$ make
gcc -g -Wall -std=gnu99 -m32 -c foo.c
gcc -g -Wall -std=gnu99 -m32 -c libstack.c
gcc -g -Wall -std=gnu99 -m32 -o foo foo.o libstack.o

$ ./foo
0x8ecc008: 0x0        0x0        0x0        0x0
0x8ecc008: 0x0        0x0        0x0        0x8ecc008
0x8ecc008: 0x0        0x0        0x8ecc00c  0x8ecc008
0x8ecc008: 0x0        0x8ecc010  0x8ecc00c  0x8ecc008
0x8ecc008: 0x8ecc014  0x8ecc010  0x8ecc00c  0x8ecc008

 (pop) got 0x8ecc014
 (pop) got 0x8ecc010
 (pop) got 0x8ecc00c
 (pop) got 0x8ecc008
$

测试简单且直接，不解释。如果还不确信，可以用gdb调试。

现在对上一篇blog末尾的递归函数使用上面实现的stack进行去递归化改写，改写后的代码如下：

void
bst_walk(bst_node_t *root)
{
    if (root == NULL)
        return;

    (void) stack_init(STACK_SIZE);

    while (root != NULL || !stack_isEmpty()) {
        if (root != NULL) {
            push((uintptr_t)root);
            root = root->left;
            continue;
        }

        pop((uintptr_t *)(&root));
        printf("%d
", root->key);

        root = root->right;
    }

    stack_fini();
}

为方便阅读，下面给出使用meld进行diff后的截图，

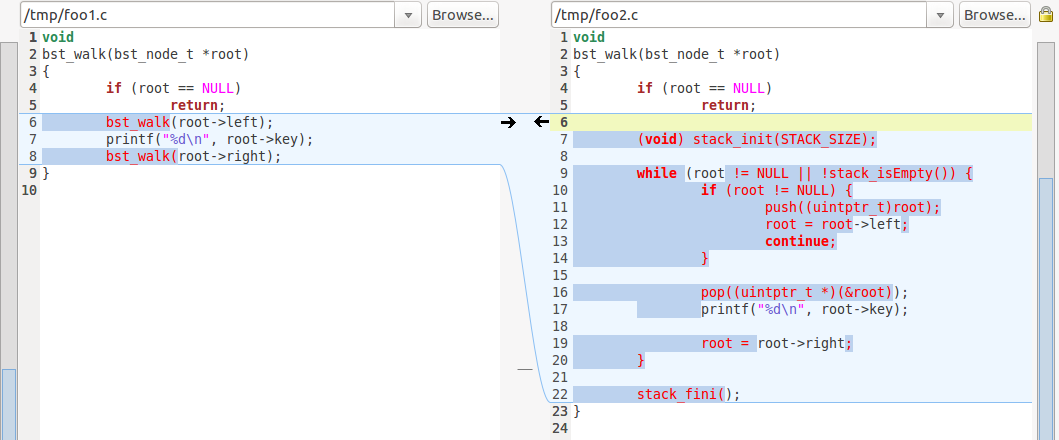
• L7: 构建一个stack, 其中STACK_SIZE是一个宏
  
• L22: 将stack销毁
• L9-14: 首先遍历左子树，不断将结点压入栈中，直到到达最左的叶子结点，那么则执行L16-17 （最左的叶子结点也会被压入栈中）
  
• L16-17: 出栈并打印结点的key
• L19: 将新的根结点设置为刚刚出栈的结点的右儿子， 重新执行L9-17， 直到所有结点都被遍历到(当然, stack为空)

注： 左图中的函数使用了两次递归，所以将其转化成非递归函数的难度相对较大。