转自https://zhuanlan.zhihu.com/p/95429428
*四种频率包括以下四个：
1、模拟频率f
2、模拟角频率Ω
3、数字频率w(归一化频率)
其中，前两种是模拟频率，是自然界中的一种物理现象，真实存在，比如风扇1秒钟转10次，则其(模拟)频率f=10Hz，Hz=1/s；也即信号在一秒钟内重复的次数。便于理解，假设一个点在单位圆上运动，如图1所示，点在圆上一秒钟转10圈，则该点的运动频率为10Hz。
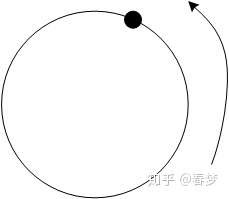图1.点在圆上运动
而模拟角频率Ω，是以弧度来表征转的圈数，一圈是2π弧度，则该点的运动频率也可表示为2π10rad/s，由此可以看出，Ω = 2*π*f。注意模拟角频率的单位是rad/s。
数字频率w的出现，是对模拟信号进行采样后，用来表示得到的数字信号。数字频率w与采样频率fs（ws）相关。
数字频率是对模拟频率的采样，数字频率代表的是两个采样点之间的间隔。还是以一点在圆上运动为例，1秒钟转动10圈，从该点运动开始，以1秒钟采样100次进行采样，可以得到，每次采样都可得到该点在圆上的位置，该点在圆上的位置如图2所示，采样点之间存在间隔，要以弧度w表示这种间隔，w = 2π10/100,可得到w = 0.2π rad。
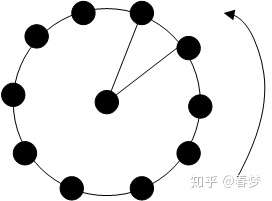图2.采样得到的点的位置
数字频率为
w = 2πf/fs = Ω/fs = ΩTs=2πΩ/ws
根据奈奎斯特定理，ws>=2Ω，因此，w<=π。由公式可以看出，数字频率是模拟频率针对采样频率的归一。
对于模拟信号
x(t) = sin(2π*10*t)
进行采样，fs = 50,采样间隔Ts = 1/50 s，自变量不再连续，由连续的时间t变为离散的变量n。假设t在某一时刻，t = 3/50 s，可以采集到的时刻包括0、1/50、2/50、3/50,.......。n即表示第几个采样点，第n个采样点对应的时刻为
t = n/50 = n*Ts
，则得到的数字信号为;
x(n) = sin(2π*10*n/50) = sin(2π*0.2*n)
此时w = 2π*0.2，fs = 50表示1s内对信号等间隔取50个点，n表示第几个点。n = (1:N)/50。
如果采样频率是fs = 100,则得到数字信号为：
x[n] = sin(2π*10*n/100) = sin(2π*0.1*n)
此时w = 2π*0.1，fs=100，表示1s内对信号等间隔取100个点。n =(1:N)/100。
可以看出，不同采样频率下的数字信号的数字频率是不同的，但是表示的是相同的信号，在理论上满足奈奎斯特定理，所包含的信息是完全相同的，还应注意到，不同采样率下，n的间隔不同。
PS:
最近设计FIR滤波器，碰到数字频率，感觉忘了，重新学习一下，比如对设计低通滤波器，其fs = 10000Hz,截止频率为500Hz，则对应的数字频率为wstop = 2π*(500/10000)=0.1π。
模拟频率、数字频率、模拟角频率之间的关系
数字频率和角频率
数字频率与模拟频率相互转化：w=2*pi*f/fs
在数字信号处理的学习中，很多刚入门朋友常常为模拟频率、数字频率及其相互之间的关系所迷惑，甚至是一些已经对数字信号处理有所了解的朋友也为这个问题所困惑。
我们通常所说的频率，在没有特别指明的情况下，指的是模拟频率，其单位为赫兹(Hz)，或者为1/秒(1/s)，数学符号用f来表示。这是因为现实世界中的信号大多为模拟信号，频率是其重要的物理特性。以赫兹表示的模拟频率表示的是每秒时间内信号变化的周期数。如果用单位圆表示的话，如图1所示，旋转一圈表示信号变化一个周期，则模拟频率则指的是每秒时间内信号旋转的圈数。
图1 数字频率与模拟频率
模拟频率中还有一个概念是模拟角频率，数学符号常用Ω来表示，其单位为弧度/秒(rad/s)。从单位圆的角度看，模拟频率是每秒时间内信号旋转的圈数，每一圈的角度变化数为2pi。很显然，旋转f圈对应着2pi*f的弧度。即：
Ω=2pi*f(rad/s) (1)
数字信号大多是从模拟信号采样而得，采样频率通常用fs表示。数字频率更准确的叫法应该是归一化数字角频率，其单位为弧度(rad)，数学符号常用ω表示。即：
ω=2pi*f/fs(rad) (2)
其物理意义是相邻两个采样点之间所变化的弧度数，如图1所示。
有了公式(1)和(2)，我们就可以在模拟频率与数字频率之间随意切换。假定有一个正弦信号x[n]，其频率f=100Hz，幅度为A，初始相位为0，则这个信号用公式可以表示为：
x(t) =A*sin(2*pi*100*t)
用采样频率fs=500Hz对其进行采样，得到的数字信号x[n]为：
x[n] =A*sin(2*pi*100*n/fs)= A*sin(0.4*pi*n)
很明显，这个数字信号的频率为0.4pi。
由上述讨论可知，对应两个数字频率完全相同的信号，其模拟频率未必相同，因为这里还要考虑采样频率。这种归一化为处理带来了方便，但也给理解带来了困惑。在数字信号中，虽然经常不显式地出现采样频率，但它却是架起模拟信号与数字信号的桥梁，对信号处理的过程有举足轻重的影响。
