时间复杂度:定性描述算法的运行时间,用O符号来表示,O(1),O(n),O(n2)等来表示数据结构的规模与计算操作所需时间的关系
React 的diff算法 时间复杂度从O(n3) 优化到 O(n) ,n表示树的所有节点数
1. Diff算法 => O(n^3) => 将两个DOM树的所有节点两两对比,时间复杂度 O(n^2)
prev last
A A
/ /
D B => B D
/
C C
所有节点两两相互对比:
pA => lA
pA => lB
pA => lD
pA => lC
...
pC => lC
再进行树的编辑(插入、替换、删除)需要遍历一次,因此时间复杂度为 O(n^3)
2. React Diff算法 => O(n) => 简单粗暴,所有的节点按层级比较,只会遍历一次
# 按叶子节点位置比较
[0,0] : pA => lA #相同,不理会
[0.0,0.0] : pD => lB #不同,删除pD,添加lB
[0.1,0.1] : pB => lD #不同,删除pB,添加lD
[0.1.0,0.1.0] : pC => Null #last树没有该节点,直接删除pC
[0.1.2,0.1.2] : Null => lC #prev树没有该节点,添加lC到该位置
React认为:一个ReactElement的type不同,那么内容基本不会复用,所以直接删除节点,
添加新节点,这是一个非常大的优化,大大减少了对比时间复杂度。
详解:
React的diff算法
(1)什么是调和?
将Virtual DOM树转换成actual DOM树的最少操作的过程 称为 调和 。
(2)什么是React diff算法?
diff算法是调和的具体实现。
diff策略
React用 三大策略 将O(n^3)复杂度 转化为 O(n)复杂度
策略一(tree diff):
Web UI中DOM节点跨层级的移动操作特别少,可以忽略不计。
策略二(component diff):
拥有相同类的两个组件 生成相似的树形结构,
拥有不同类的两个组件 生成不同的树形结构。
策略三(element diff):
对于同一层级的一组子节点,通过唯一id区分。
(1)React通过updateDepth对Virtual DOM树进行层级控制。
(2)对树分层比较,两棵树 只对同一层次节点 进行比较。如果该节点不存在时,则该节点及其子节点会被完全删除,不会再进一步比较。
(3)只需遍历一次,就能完成整棵DOM树的比较
答:diff只简单考虑同层级的节点位置变换,如果是跨层级的话,只有创建节点和删除节点的操作。
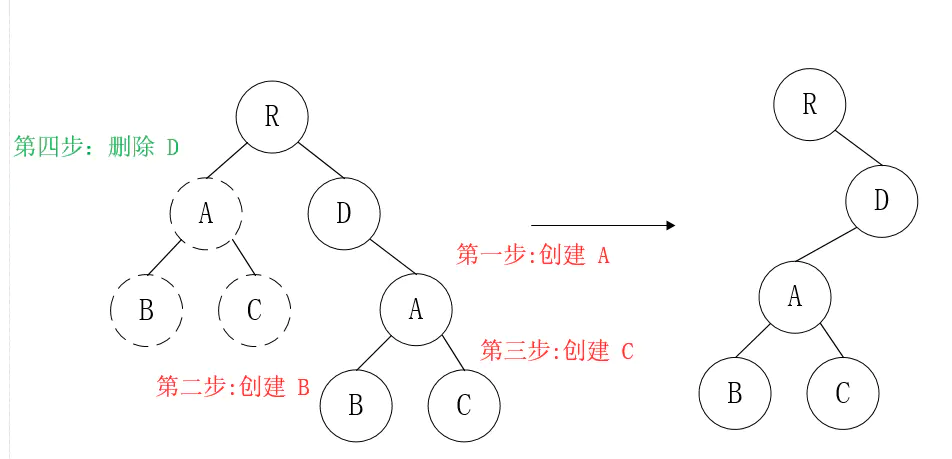
如上图所示,以A为根节点的整棵树会被重新创建,而不是移动,因此 官方建议不要进行DOM节点跨层级操作,可以通过CSS隐藏、显示节点,而不是真正地移除、添加DOM节点。
component diff
React对不同的组件间的比较,有三种策略
(1)同一类型的两个组件,按原策略(层级比较)继续比较Virtual DOM树即可。
(2)同一类型的两个组件,组件A变化为组件B时,可能Virtual DOM没有任何变化,如果知道这点(变换的过程中,Virtual DOM没有改变),可节省大量计算时间,所以 用户 可以通过 shouldComponentUpdate() 来判断是否需要 判断计算。
(3)不同类型的组件,将一个(将被改变的)组件判断为dirty component(脏组件),从而替换 整个组件的所有节点。
注意:如果组件D和组件G的结构相似,但是 React判断是 不同类型的组件,则不会比较其结构,而是删除 组件D及其子节点,创建组件G及其子节点。
element diff
当节点处于同一层级时,diff提供三种节点操作:删除、插入、移动。
插入:组件 C 不在集合(A,B)中,需要插入
删除:(1)组件 D 在集合(A,B,D)中,但 D的节点已经更改,不能复用和更新,所以需要删除 旧的 D ,再创建新的。
(2)组件 D 之前在 集合(A,B,D)中,但集合变成新的集合(A,B)了,D 就需要被删除。
移动:组件D已经在集合(A,B,C,D)里了,且集合更新时,D没有发生更新,只是位置改变,如新集合(A,D,B,C),D在第二个,无须像传统diff,让旧集合的第二个B和新集合的第二个D 比较,并且删除第二个位置的B,再在第二个位置插入D,而是 (对同一层级的同组子节点) 添加唯一key进行区分,移动即可。
情形一:新旧集合中存在相同节点但位置不同时,如何移动节点
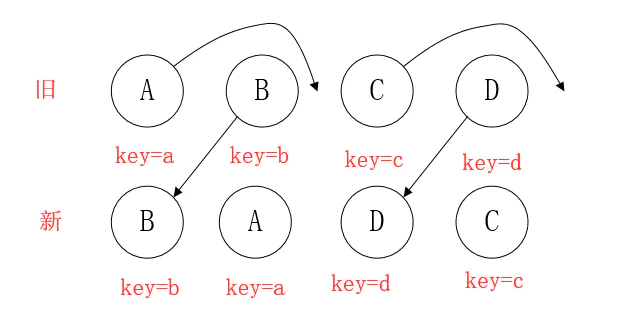
(1)看着上图的 B,React先从新中取得B,然后判断旧中是否存在相同节点B,当发现存在节点B后,就去判断是否移动B。
B在旧 中的index=1,它的lastIndex=0,不满足 index < lastIndex 的条件,因此 B 不做移动操作。此时,一个操作是,lastIndex=(index,lastIndex)中的较大数=1.
注意:lastIndex有点像浮标,或者说是一个map的索引,一开始默认值是0,它会与map中的元素进行比较,比较完后,会改变自己的值的(取index和lastIndex的较大数)。
(2)看着 A,A在旧的index=0,此时的lastIndex=1(因为先前与新的B比较过了),满足index<lastIndex,因此,对A进行移动操作,此时lastIndex=max(index,lastIndex)=1。
(3)看着D,同(1),不移动,由于D在旧的index=3,比较时,lastIndex=1,所以改变lastIndex=max(index,lastIndex)=3
(4)看着C,同(2),移动,C在旧的index=2,满足index<lastIndex(lastIndex=3),所以移动。
由于C已经是最后一个节点,所以diff操作结束。
情形二:新集合中有新加入的节点,旧集合中有删除的节点
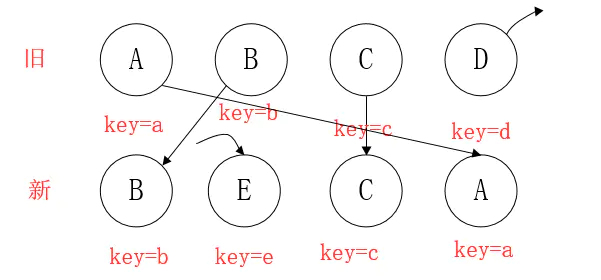
1)B不移动,不赘述,更新l astIndex=1
(2)新集合取得 E,发现旧不存在,故在lastIndex=1的位置 创建E,更新lastIndex=1
(3)新集合取得C,C不移动,更新lastIndex=2
(4)新集合取得A,A移动,同上,更新lastIndex=2
(5)新集合对比后,再对旧集合遍历。判断 新集合 没有,但 旧集合 有的元素(如D,新集合没有,旧集合有),发现 D,删除D,diff操作结束。
diff的不足与待优化的地方

看图的 D,此时D不移动,但它的index是最大的,导致更新lastIndex=3,从而使得其他元素A,B,C的index<lastIndex,导致A,B,C都要去移动。
理想情况是只移动D,不移动A,B,C。因此,在开发过程中,尽量减少类似将最后一个节点移动到列表首部的操作,当节点数量过大或更新操作过于频繁时,会影响React的渲染性能。
转载:https://www.jianshu.com/p/3ba0822018cf