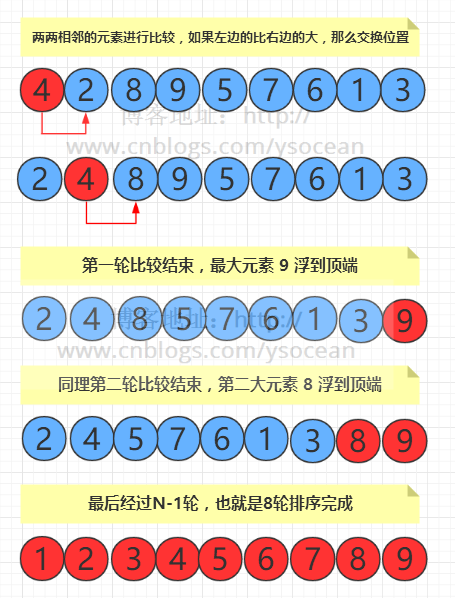
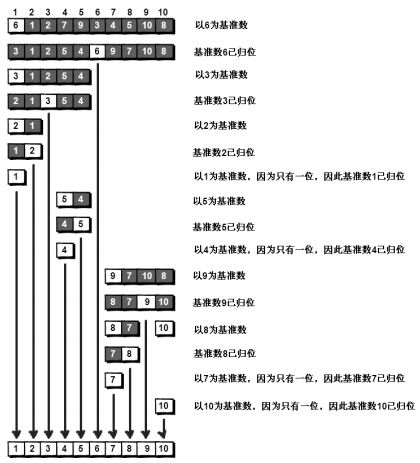
冒泡排序:首轮冒泡后最大的元素在最右边,次轮最大的元素在倒二,最终得到有序的数据
复杂度:(N-1)+(N-2)+...+1 = N*(N-1)/2,数据量较大的时候是 O(N2) 时间级别。
选择排序:每一次从待排序的数据元素中选出最小的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
复杂度:N*(N-1)/2,数据量较大的时候是 O(N2) 时间级别。

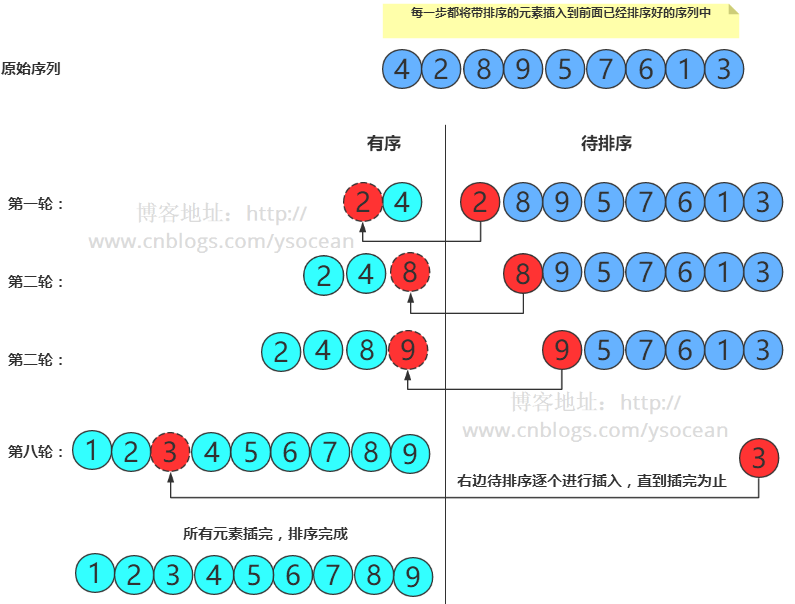
插入排序:每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
复杂度:对大致有序的数据性能高,否知性能低
递归:在运行的过程中调用自己。
/** * 0!=1 1!=1 * 负数没有阶乘,如果输入负数返回-1 * @param n * @return */ public static int getFactorialFor(int n){ int temp = 1; if(n >=0){ for(int i = 1 ; i <= n ; i++){ temp = temp*i; } }else{ return -1; } return temp; }
二分查找:查找的数组一定是有序的才行

分治法:当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。这就是分治策略的基本思想。
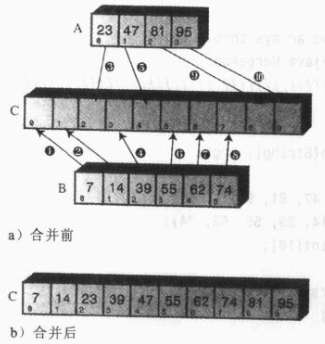
归并排序:归并两个已经有序的数组,归并两个有序数组A和B,就生成了第三个有序数组C。数组C包含数组A和B的所有数据项。
public static int[] mergeSort(int[] c,int start,int last){ if(last > start){ //也可以是(start+last)/2,这样写是为了防止数组长度很大造成两者相加超过int范围,导致溢出 int mid = start + (last - start)/2; mergeSort(c,start,mid);//左边数组排序 mergeSort(c,mid+1,last);//右边数组排序 merge(c,start,mid,last);//合并左右数组 } return c; } public static void merge(int[] c,int start,int mid,int last){ int[] temp = new int[last-start+1];//定义临时数组 int i = start;//定义左边数组的下标 int j = mid + 1;//定义右边数组的下标 int k = 0; while(i <= mid && j <= last){ if(c[i] < c[j]){ temp[k++] = c[i++]; }else{ temp[k++] = c[j++]; } } //把左边剩余数组元素移入新数组中 while(i <= mid){ temp[k++] = c[i++]; } //把右边剩余数组元素移入到新数组中 while(j <= last){ temp[k++] = c[j++]; } //把新数组中的数覆盖到c数组中 for(int k2 = 0 ; k2 < temp.length ; k2++){ c[k2+start] = temp[k2]; } }
消除递归:大多数都是用栈来实现递归的。
希尔排序
直接插入排序,首先我们将需要插入的数放在一个临时变量中,这也是一个标记符,标记符左边的数是已经排好序的,标记符右边的数是需要排序的。接着将标记的数和左边排好序的数进行比较,假如比目标数大则将左边排好序的数向右边移动一位,直到找到比其小的位置进行插入。这里就存在一个效率问题了,如果一个很小的数在很靠近右边的位置,比如上图右边待排序的数据 1 ,那么想让这个很小的数 1 插入到左边排好序的位置,那么左边排好序的数据项都必须向右移动一位,这个步骤就是将近执行了N次复制,虽然不是每个数据项都必须移动N个位置,但是每个数据项平均移动了N/2次,总共就是N2/2,因此插入排序的效率是O(N2)。
快速排序
对冒泡排序的一种改进,采用的是分治策略(一般与递归结合使用),以减少排序过程中的比较次数:
一、先通过第一趟排序,将数组原地划分为两部分,其中一部分的所有数据都小于另一部分的所有数据。原数组被划分为2份
二、通过递归的处理, 再对原数组分割的两部分分别划分为两部分,同样是使得其中一部分的所有数据都小于另一部分的所有数据。 这个时候原数组被划分为了4份
三、就1,2被划分后的最小单元子数组来看,它们仍然是无序的,但是! 它们所组成的原数组却逐渐向有序的方向前进。
四、这样不断划分到最后,数组就被划分为多个由一个元素或多个相同元素组成的单元,这样数组就有序了。
这里涉及到基准元素,左游标,右游标三个概念。
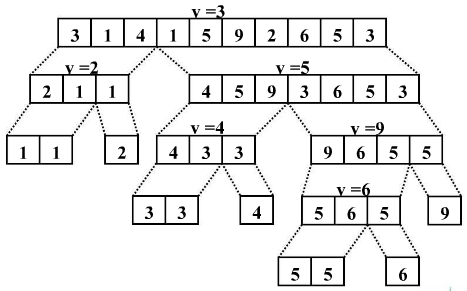
下面用生动的图片来描述:

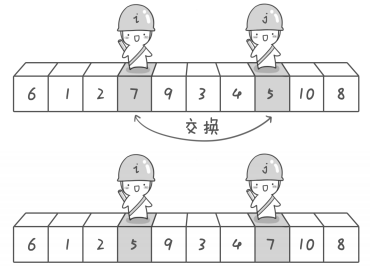


public class QuickSort { //数组array中下标为i和j位置的元素进行交换 private static void swap(int[] array , int i , int j){ int temp = array[i]; array[i] = array[j]; array[j] = temp; } private static void recQuickSort(int[] array,int left,int right){ if(right <= left){ return;//终止递归 }else{ int partition = partitionIt(array,left,right); recQuickSort(array,left,partition-1);// 对上一轮排序(切分)时,基准元素左边的子数组进行递归 recQuickSort(array,partition+1,right);// 对上一轮排序(切分)时,基准元素右边的子数组进行递归 } } private static int partitionIt(int[] array,int left,int right){ //为什么 j加一个1,而i没有加1,是因为下面的循环判断是从--j和++i开始的. //而基准元素选的array[left],即第一个元素,所以左游标从第二个元素开始比较 int i = left; int j = right+1; int pivot = array[left];// pivot 为选取的基准元素(头元素) while(true){ while(i<right && array[++i] < pivot){} while(j > 0 && array[--j] > pivot){} if(i >= j){// 左右游标相遇时候停止, 所以跳出外部while循环 break; }else{ swap(array, i, j);// 左右游标未相遇时停止, 交换各自所指元素,循环继续 } } swap(array, left, j);//基准元素和游标相遇时所指元素交换,为最后一次交换 return j;// 一趟排序完成, 返回基准元素位置(注意这里基准元素已经交换位置了) } public static void sort(int[] array){ recQuickSort(array, 0, array.length-1); } //测试 public static void main(String[] args) { //int[] array = {7,3,5,2,9,8,6,1,4,7}; int[] array = {9,9,8,7,6,5,4,3,2,1}; sort(array); for(int i : array){ System.out.print(i+" "); } //打印结果为:1 2 3 4 5 6 7 7 8 9 } }
优化:对快速排序来说,拥有两个大小相等的子数组是最优的情况,为了找到一个数组中的中值数据,一般是取数组中第一个、中间的、最后一个,选择这三个数中位于中间的数。