[抄题]:
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
[一句话思路]:
找第k个元素,而且不得不丢掉前k/2个,拿肯定是丢小的。
[画图]:
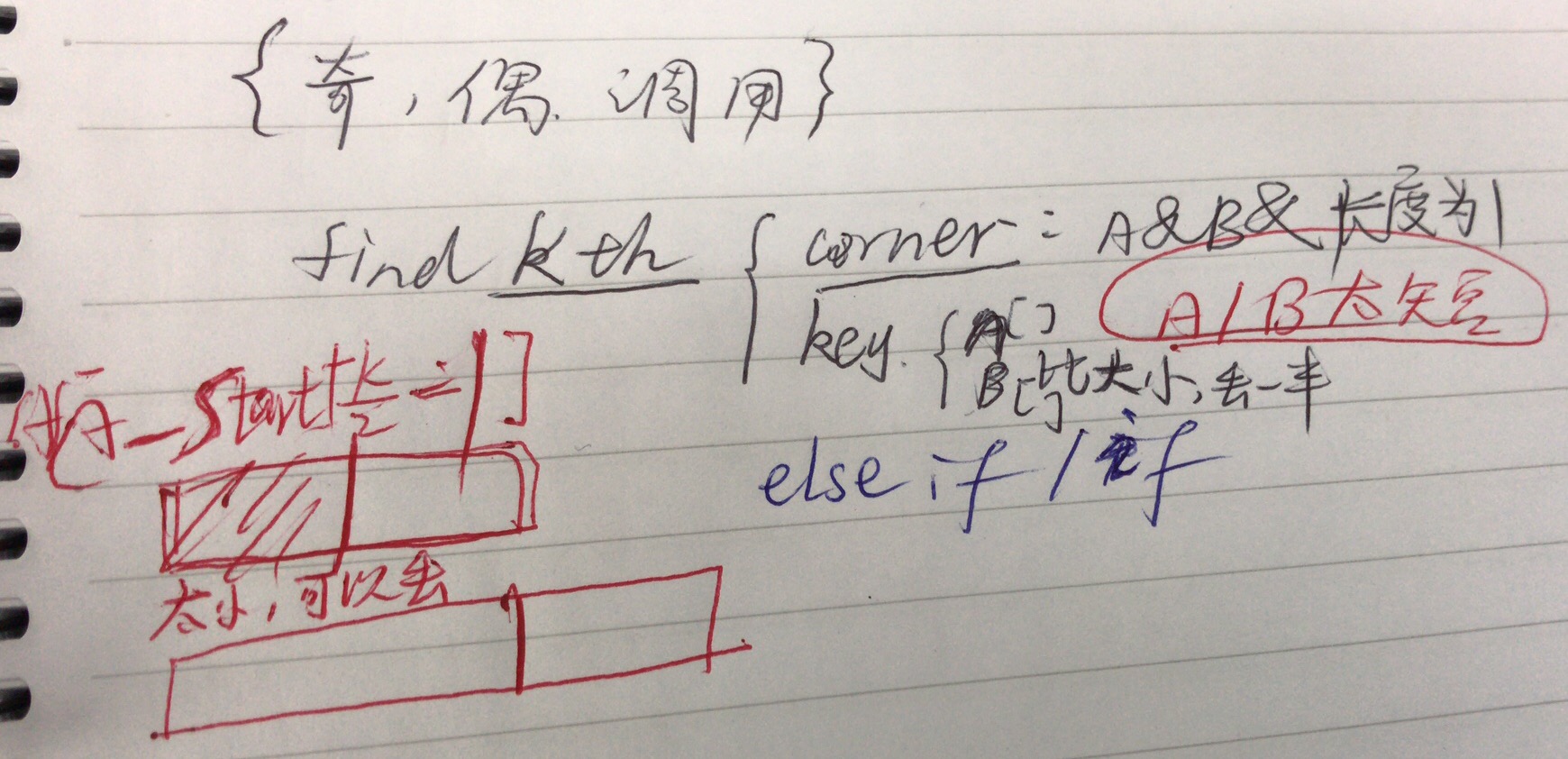
[一刷]:
- 用A_start A.length比较长度,看表示数组空不空,因为调用后A_start会改变
- A_key,B_key都是数组元素,不是index。因为相互比较的时候,index小的,数值不一定小。
- 函数声明里面要有数据类型 int[] nums, int k 之类的
- 能用if else就用。因为a>b之外的情况,如果写两次,就很麻烦。
[总结]:
丢掉小的一半,看图。
[复杂度]:
[英文数据结构]:
[其他解法]:
[题目变变变]:

class Solution { public double findMedianSortedArrays(int[] nums1, int[] nums2) { int len = nums1.length + nums2.length; if (len % 2 == 1) { return findKth(nums1, 0, nums2, 0, len / 2 + 1); } else { return ( findKth(nums1, 0, nums2, 0, len / 2 + 1) + findKth(nums1, 0, nums2, 0, len / 2) ) / 2; } } private double findKth(int[] A, int A_start, int[] B, int B_start, int k) { //corner case if (A_start >= A.length) { return B[B_start + k -1]; } if (B_start >= B.length) { return A[A_start + k -1]; } if (k == 1) { return Math.min(A[A_start], B[B_start]); } //useless key? int A_key = A_start + k / 2 -1 < A.length ? A[A_start + k / 2 -1] : Integer.MAX_VALUE; int B_key = B_start + k / 2 -1 < B.length ? B[B_start + k / 2 -1] : Integer.MAX_VALUE; //compare key if (A_key < B_key) { return findKth(A, A_start + k / 2, B, B_start, k - k / 2); } else { return findKth(A, A_start, B, B_start + k / 2, k - k / 2); } } }
