1.群:封闭性,结合律,单位元,逆元;可交换,交换群;|S|<正无穷,有限群
2.模n加法群(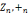 ),|
),|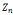 |=n;是有限可交换群(0~n-1)
|=n;是有限可交换群(0~n-1)
3.模n乘法群(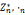 ),该群中的元素是
),该群中的元素是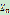 中与n互为质数的元素组成的集合
中与n互为质数的元素组成的集合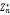
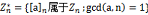
4.模n乘法群( ),是有限可交换群
),是有限可交换群
证明逆元:
a是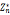 中的一个元素, EXTEND-EXCULID(a,n),d=1
中的一个元素, EXTEND-EXCULID(a,n),d=1
ax+ny=1 即 ax=1(modn) 即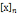 是
是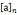 模n的乘法逆元
模n的乘法逆元
5.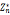 的规模为φ(n),为欧拉phi函数,满足:
的规模为φ(n),为欧拉phi函数,满足:
φ(n)=n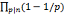
p是素数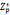 的规模φ(n)=p-1
的规模φ(n)=p-1
n是合数,φ(n)<n-1
6.子群:有限群的非空封闭子集
7.拉格朗日定理:S是一个有限群,S`是一个子群,|S`|是|S|的一个约数
8.S`是S的一个真子群,|S`|<=|S|/2
9.在群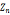 中,
中,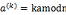 ;在群
;在群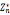 中,
中,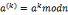 由a生成的子群 <a>={
由a生成的子群 <a>={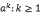 },a是<a>的生成元
},a是<a>的生成元
10.一个元素的阶等于它生成子群的规模即ord(a)=|<a>|,即满足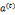 =e的最小正整数t
=e的最小正整数t
11.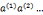 是周期性序列,周期为t=ord(a),即
是周期性序列,周期为t=ord(a),即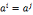 当且仅当i=j(modt)
当且仅当i=j(modt)
12.S是有单位元e的有限群,对任意a属于S,则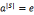
证明:由拉格朗日定理知:|ord(a)|||S|,所以,S=0(mod |ord(a)|),所以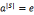
其实就一句话,|S|是ord(a)的倍数,a的ord(a)次方必为e,故~