参考链接:http://sebastianruder.com/optimizing-gradient-descent/
如果熟悉英文的话,强烈推荐阅读原文,毕竟翻译过程中因为个人理解有限,可能会有谬误,还望读者能不吝指出。另外,由于原文太长,分了两部分翻译,本篇主要是梯度下降优化算法的总结,下篇将会是随机梯度的并行和分布式,以及优化策略的总结。
梯度下降是优化中最流行的算法之一,也是目前用于优化神经网络最常用到的方法。同时,每个优秀的深度学习库都包含了优化梯度下降的多种算法的实现(比如, lasagne 、 caffe 和 keras 的文档)。然而,这些算法一般被封装成优化器,如黑盒一般,因此很难得到它们实际能力和缺点的解释。
本篇博客的目标是为读者提供不同梯度下降优化算法的直观解释,希望读者可以学以致用。我们会先了解下梯度下降的不同变种。然后会对训练过程的问题进行简单总结。接着,我们会介绍最常用的优化算法,展示它们解决这些问题的动机,以及它们对应更新规则变化的原因。我们也就会简单回顾在并行和分布式的情况下,梯度下降优化的算法和架构。最后,我们也会聊聊有助于优化梯度下降的其他策略。
梯度下降是最小化以模型参数 θ∈Rdθ∈Rd 构建的目标函数 J(θ)J(θ) 的一种方法,它通过按目标函数 ∇θJ(θ)∇θJ(θ) 在参数梯度的相反方向更新参数。学习率 ηη 决定了我们到达(局部)最小所需的步数的大小。换成通俗的话说,我们会沿着目标函数所构建的表面坡度的方向往下走,直到我们到达一个谷底。如果你还不熟悉梯度下降,你可以参考这篇 优化神经网络的入门介绍 。
不同版本的梯度下降
一共有三种不同版本的梯度下降,它们的不同之处字啊与我们计算目标函数梯度时使用数据的多少。根据数据量的大小,我们会在参数更新的准确度和更新花费的时间之间进行权衡。
批量梯度下降
最普通的梯度下降,即批量梯度下降,使用整个训练数据根据参数 θθ 计算目标函数的梯度:
θ=θ−η⋅∇θJ(θ)θ=θ−η⋅∇θJ(θ)
因为我们需要计算完整个数据集的梯度才能更新,批量梯度下降非常的耗时,而且面对无法完全放入内容的数据集,处理起来也很棘手。批量梯度更新也无法让我们 在线 ,即在运行时加入新的样本进行模型更新。
以代码的形式,批量梯度下降的形式如下:
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
对于预先设定好的训练迭代次数,我们首先对于整个数据集根据参数矢量 params 计算损失函数的梯度矢量 weight_grad 。注意最新的深度学习库提供了自动微分的方法,可以根据参数高效计算梯度。如果你自己做梯度的微分,那么最好做一下梯度检查。(从 这篇文章 可以获取一些合理检查梯度的技巧。)
SGD 的代码片段仅仅在训练样本时添加了一个循环,根据每个样本进行梯度估计。注意我们会在每次更新训练时会对训练数据进行随机洗牌处理,这会在后面进行解释:
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad
挑战
然而, 传统的 mini-batch 梯度下降,并无法保证好的收敛,但却有一些需要强调的挑战:
- 选择一个合适的学习率很困难。学习率太小导致收敛巨慢,而学习率过大又会妨碍收敛,导致损失函数在最小值附件波动,甚至发散出去。
- 学习率的调度 11 尝试使用如模拟退火等方法在训练时可以根据预先定义的调度方式,或者当两次训练中目标的变化在阈值之下时,可以自动的调整学习率。然而,这些调度方式和阈值需要提前定义,因此无法适用于数据集的特征 10 。
- 另外,同一个学习率应用到所有的参数更新。如果我们的数据非常稀疏,特征具有完全不同的频率,我们可能不希望以相同的方式对它们进行更新,更希望对少量出现的特征进行较大的更新。
- 另一个关键的挑战在于最小化神经网络中常见的非凸误差函数时,要避免陷入大量的局部最小值。Dauphin et al.声称实际上难度并非由局部最小值引起,而是由鞍点导致,鞍点就是那些在一个维度是上坡,另一个维度是下坡的点。这些鞍点一般由稳定的相同错误值围绕,这就让 SGD 很难从鞍点逃逸,因为梯度在各个维度都接近于零。
梯度下降优化算法
接下来,我们将会罗列一些深度学习社区广泛用于处理前面提到的挑战的算法。我们将不会讨论那些无法实际处理高维数据集的算法,即二阶方法,如 牛顿法 。






二、关于solver.prototxt中相关参数的解释:
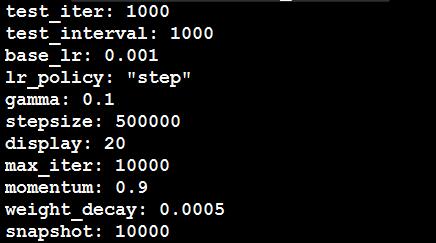
epoch:1个epoch就是将所有的训练图像全部通过网络训练一次
例如:假如有1280000张图片,batchsize=256,则1个epoch需要1280000/256=5000次iteration
它的max-iteration=450000,则共有450000/5000=90个epoch
而lr什么时候衰减与stepsize有关,减少多少与gamma有关,即:若stepsize=500, base_lr=0.01, gamma=0.1,则当迭代到第一个500次时,lr第一次衰减,衰减后的lr=lr*gamma=0.01*0.1=0.001,以后重复该过程,所以
stepsize是lr的衰减步长,gamma是lr的衰减系数。
在训练过程中,每到一定的迭代次数都会测试,迭代次数是由test-interval决定的,如test_interval=1000,则训练集每迭代1000次测试一遍网络,而
test_size, test_iter, 和test图片的数量决定了怎样test, test-size决定了test时每次迭代输入图片的数量,test_iter就是test所有的图片的迭代次数,如:500张test图片,test_iter=100,则test_size=5, 而solver文档里只需要根据test图片总数量来设置test_iter,以及根据需要设置test_interval即可。
三、关于train.prototxt中相关系数解释:
name: "LeNet"
layer {
name: "mnist"
type: "Data" //这里的type还有MemoryData(内存读取)HDF5Date,HDF5output,ImageDta等
top: "data" //bottom代表输入,top代表输出
top: "label"
include {
phase: TRAIN //该层参数只在训练阶段有效
}
transform_param {
scale: 0.00390625 //数据变换使用的数据缩放因子,用于数据预处理如剪均值,尺寸变换,随机剪,镜像等
}
data_param { //数据层参数
source: "./examples/mnist/mnist_train_lmdb" #lmdb路径
batch_size: 64 //批量数目,一次读取64张图
backend: LMDB
}
}
layer { //一个新的数据层,但只在测试阶段才有效
name: "mnist"
type: "Data"
top: "data"
top: "label"
include {
phase: TEST //该层参数只在测试阶段有效
}
transform_param {
scale: 0.00390625
}
data_param {
source: "./examples/mnist/mnist_test_lmdb"
batch_size: 100
backend: LMDB
}
}
layer { //定义接下来的卷积层
name: "conv1"
type: "Convolution"
bottom: "data" //输入为data
top: "conv1" //输出为conv1
param {
lr_mult: 1 //weights的学习率和全局相同
}
param {
lr_mult: 2 //biases的学习率是全局的2倍
}
convolution_param { //卷积计算参数
num_output: 20 //输出特征图数量为20,即有20个filters
kernel_size: 5 //卷积核的尺寸为5*5,这里的卷积核即为filter
stride: 1 //卷积核移动尺寸
weight_filler { //权值使用xavier填充器
type: "xavier" //一种初始化方法
}
bias_filler { //bias使用常数填充器,默认为0
type: "constant"
}
}
}
layer { //定义接下来的池化层(又称下采样层)
name: "pool1"
type: "Pooling"
bottom: "conv1"
top: "pool1"
pooling_param {
pool: MAX //使用最大值下采样法
kernel_size: 2 //下采样窗口尺寸为2*2
stride: 2 //窗口移动尺寸为2
}
}
layer {
name: "conv2"
type: "Convolution"
bottom: "pool1"
top: "conv2"
param {
lr_mult: 1
}
param {
lr_mult: 2
}
convolution_param {
num_output: 50
kernel_size: 5
stride: 1
weight_filler {
type: "xavier"
}
bias_filler {
type: "constant"
}
}
}
layer {
name: "pool2"
type: "Pooling"
bottom: "conv2"
top: "pool2"
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layer { //全连接层
name: "ip1"
type: "InnerProduct"
bottom: "pool2"
top: "ip1"
param {
lr_mult: 1
}
param {
lr_mult: 2
}
inner_product_param {
num_output: 500 //该层输出元素个数为500个
weight_filler {
type: "xavier"
}
bias_filler {
type: "constant"
}
}
}
layer { //非线性层,使用RELU激活函数
name: "relu1"
type: "ReLU"
bottom: "ip1"
top: "ip1"
}
layer {
name: "ip2"
type: "InnerProduct"
bottom: "ip1"
top: "ip2"
param {
lr_mult: 1
}
param {
lr_mult: 2
}
inner_product_param {
num_output: 10
weight_filler {
type: "xavier"
}
bias_filler {
type: "constant"
}
}
}
layer { //分类准确率层,只在TEST阶段有效,输出为accuracy,该层用于计算准确率
name: "accuracy"
type: "Accuracy"
bottom: "ip2"
bottom: "label"
top: "accuracy"
include {
phase: TEST
}
}
layer { //损失层,采用softmax分类器计算loss值
name: "loss"
type: "SoftmaxWithLoss"
bottom: "ip2"
bottom: "label"
top: "loss"
}
momentum:动量(又称动量衰减系数)

weight_decay:正则化惩罚项的系数
总结:
(1)SGD
优点:简单方便;
缺点:1、选择一个合适的学习率很难;2、对于稀疏数据,每个都是同等的更新,但可能存在就是某些数据需要更多更新,某些只要fintune即可;3、容易陷入局部最小值;
(2)SGD with momentum
优点:更新时可以保留之前更新的方向,所以下降时具有惯性更快,且有一定几率逃出局部最小值;
(3)Nexterov 动量下降
优点:不像传统的momentum那样根据惯性来下降,而是根据参数的近似未来位置来更新,更加准确智能;
(4)Adagrad下降
优点:根据参数自适应地更新学习率,对于不断频繁更新的参数作较大更新,对于很少更新的参数作作较小更新,所以我们不需要手动更新学习率,一般初始化为0.01;
缺点:由于分母上累积了梯度的平方,且每个加上的值都是整数,随着不断训练累积和会不断增大,导致学习率不断减小,学习能力越来越弱;
(5)Adadelta下降
优点:它是对Adagrad的扩展,解决了Adagrad激进单调递减学习率的缺点,它的梯度递归的由前面所有梯度的平方的均值来替代,同时还不需要设置初始学习率了;
(6)RMSprop下降:也是用来解决Adagrad学习率下降过快的问题;
(7)ADAM下降:比其他下降策略更好,具体看上面;
比较:
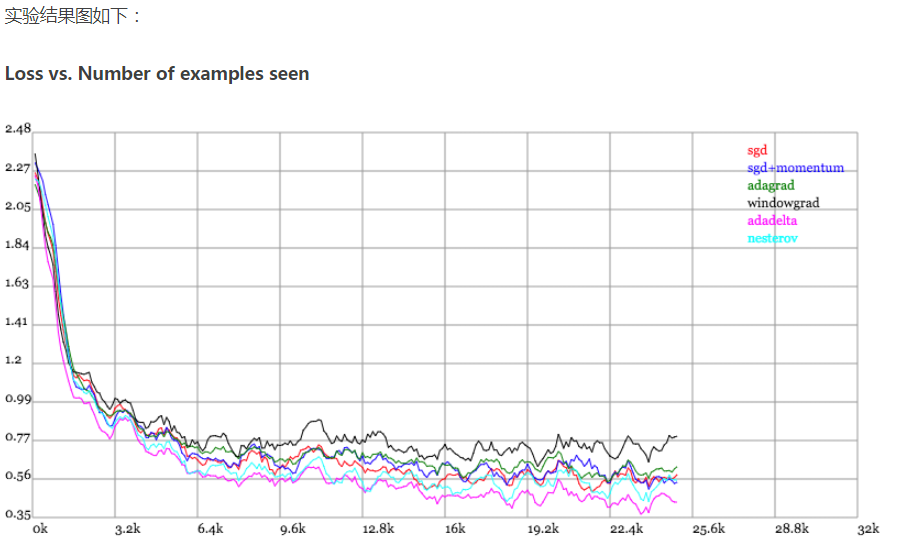
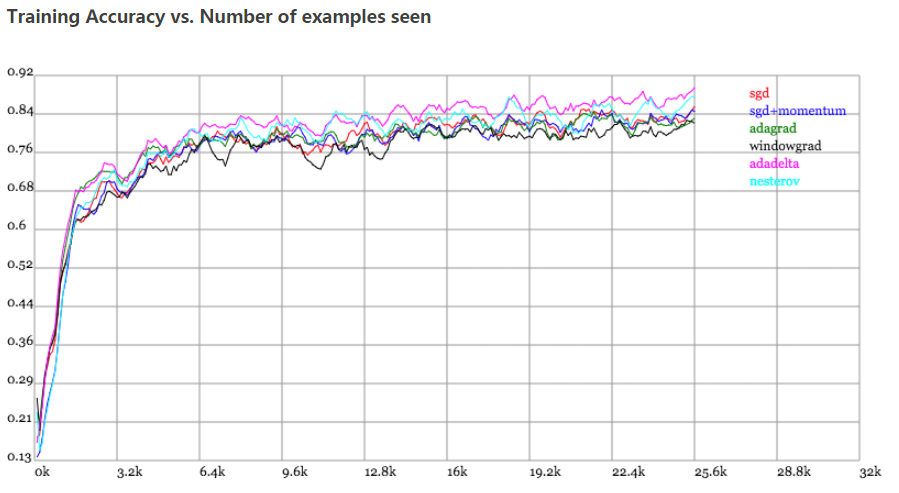
Karpathy做了一个这几个方法在MNIST上性能的比较,其结论是:
adagrad相比于sgd和momentum更加稳定,即不需要怎么调参。而精调的sgd和momentum系列方法无论是收敛速度还是precision都比adagrad要好一些。在精调参数下,一般Nesterov优于momentum优于sgd。而adagrad一方面不用怎么调参,另一方面其性能稳定优于其他方法。