算法笔记----背包九讲 ①

https://www.kancloud.cn/kancloud/pack/70125

 

题目

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

基本思路

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

用子问题定义状态：即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是：

f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}

这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下：“将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”，价值为f[i-1][v]；如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。

优化空间复杂度

以上方法的时间和空间复杂度均为O(VN)，其中时间复杂度应该已经不能再优化了，但空间复杂度却可以优化到O。

先考虑上面讲的基本思路如何实现，肯定是有一个主循环i=1..N，每次算出来二维数组f[i][0..V]的所有值。那么，如果只用一个数组f[0..V]，能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢？f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来，能否保证在推f[i][v]时（也即在第i次主循环中推f[v]时）能够得到f[i-1][v]和f[i-1][v-c[i]]的值呢？事实上，这要求在每次主循环中我们以v=V..0的顺序推f[v]，这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i-1][v-c[i]]的值。（这一部分推导见算法笔记背包问题的第第一篇文章中的i的第一次迭代结果https://www.cnblogs.com/islch/p/12567179.html）

伪代码如下：

for i=1..N
    for v=V..0
        f[v]=max{f[v],f[v-c[i]]+w[i]};

其中的f[v]=max{f[v],f[v-c[i]]}一句恰就相当于我们的转移方程f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]}，因为现在的f[v-c[i]]就相当于原来的f[i-1][v-c[i]]。如果将v的循环顺序从上面的逆序改成顺序的话，那么则成了f[i][v]由f[i][v-c[i]]推知，与本题意不符，但它却是另一个重要的背包问题P02最简捷的解决方案，故学习只用一维数组解01背包问题是十分必要的。

事实上，使用一维数组解01背包的程序在后面会被多次用到，所以这里抽象出一个处理一件01背包中的物品过程，以后的代码中直接调用不加说明。

过程ZeroOnePack，表示处理一件01背包中的物品，两个参数cost、weight分别表明这件物品的费用和价值。

procedure ZeroOnePack(cost,weight)
    for v=V..cost
        f[v]=max{f[v],f[v-cost]+weight}

注意这个过程里的处理与前面给出的伪代码有所不同。前面的示例程序写成v=V..0是为了在程序中体现每个状态都按照方程求解了，避免不必要的思维复杂度。而这里既然已经抽象成看作黑箱的过程了，就可以加入优化。费用为cost的物品不会影响状态f[0..cost-1]，这是显然的。

有了这个过程以后，01背包问题的伪代码就可以这样写：

for i=1..N
    ZeroOnePack(c[i],w[i]);

初始化的细节问题

我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。

如果是第一种问法，要求恰好装满背包，那么在初始化时除了f[0]为0其它f[1..V]均设为-∞，这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。

如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将f[0..V]全部设为0。

为什么呢？可以这样理解：初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可能被价值为0的nothing“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。

这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状态转移之前的初始化进行讲解。

一个常数优化

前面的伪代码中有 for v=V..1，可以将这个循环的下限进行改进。

由于只需要最后f[v]的值，倒推前一个物品，其实只要知道f[v-w[n]]即可。以此类推，对以第j个背包，其实只需要知道到f[v-sum{w[j..n]}]即可，后面笔记会给出解释，即代码中的

for i=1..N
    for v=V..0

可以改成

for i=1..n
    bound=max{V-sum{w[i..n]},c[i]}
    for v=V..bound

这对于V比较大时是有用的。

小结

01背包问题是最基本的背包问题，它包含了背包问题中设计状态、方程的最基本思想，另外，别的类型的背包问题往往也可以转换成01背包问题求解。故一定要仔细体会上面基本思路的得出方法，状态转移方程的意义，以及最后怎样优化的空间复杂度。

 

 

---

对这部分的笔记，略看就ok，因为有几个示意图还不错就摘录了：

 https://blog.csdn.net/TimeMagician/article/details/79731062

P1.01基础背包问题
对于N个宝石，每个宝石的价值为vi，重量花费为wi。背包的总载重量为W，则试问对于一个背包这么放宝石才能使其装的宝石总价值最大。
具体思路：考虑状态，利用i表示第i个宝石，j表示当前背包的已用空间，d[i][j]就可以表示当前状况下背包内宝石的最大价值。则要求的问题可以转化为d[N][W]的求取。
然后构建状态转移方程：

d[i][j]=max{d[i−1][j],d[i−1][j−w[i]]+v[i]}

值得注意的是这里max内只有两项是因为一个宝石只有选和不选两种情况，所以DP状态转移方程的思想就是：

当前状态 = 取最优{前一状态1，前一状态2…前一状态n}

从上可以看出状态的选取很重要，并且由于是通过将最终问题不断分为前一种状态下的最优解（即最优子结构），所以要采用自底向上的方式计算，即先计算最小问题单元，并记录，然后计算后一级问题时就可以以直接调用节约时间。所以时自底向上。也就是对解空间树从计算叶子问题开始逐步推向主问题。
仔细考虑这一过程也可以发现，在逐步上推的过程中，母问题的决策方案是不会对之前的子问题造成影响的，因此这就是无后效性的表现。（叶子问题的决策->子问题1的决策->…->子问题n的决策->母问题的决策）
伪代码为：

d[0][0...W] = 0;
for i = 1->N
    for j = 0->W
        if(w[i] > j)
            d[i][j] =d[i-1][j]
        else
            d[i][j] = max{d[i-1][j],d[i-1][j-w[i]]+v[i]}

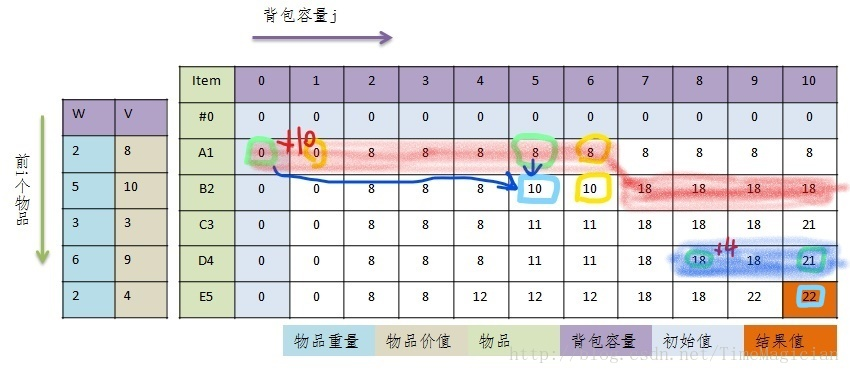
根据图示例子看下状态方程的思路：图片转自：http://www.cnblogs.com/banyu/p/4994999.html

 

 

 

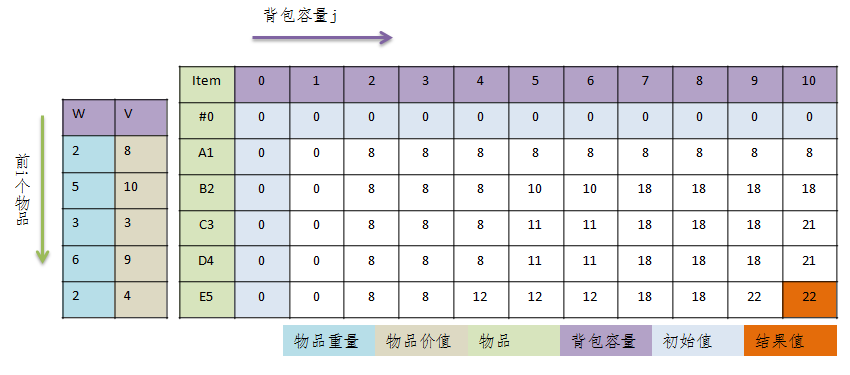
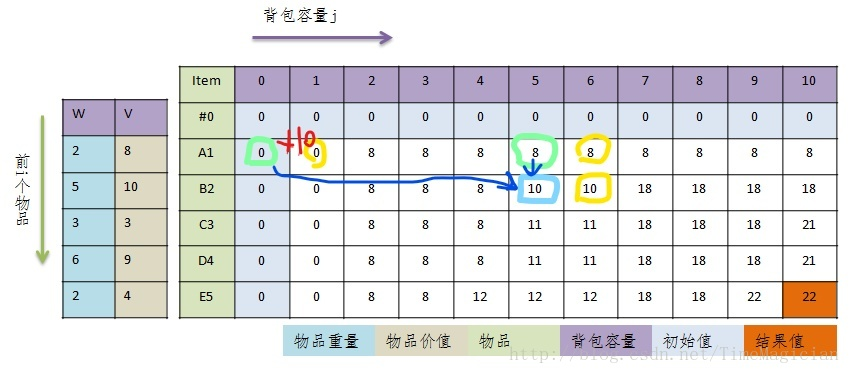
 图中青色代表d[2][5]，可以看出他由绿色的两个各种中的数值得出。即当前状态由前一状态的两个解中的最优解得出。接下来黄色的三个圈也一样。因此DP的路线就是从左上角不断计算得到右下角的最终问题的解。要注意的是DP有个赋予初值的步骤。

 

问题优化

刚好放满的求解方法

由上图看出，如果我想求解刚好放满背包时候的背包的最大价值，可以采用的方法就是初值的赋予技巧，即只对d[0][0] = 0，d[0][1…W]都赋予负无穷，这样就可以筛选掉不满的情况。

空间的优化

 

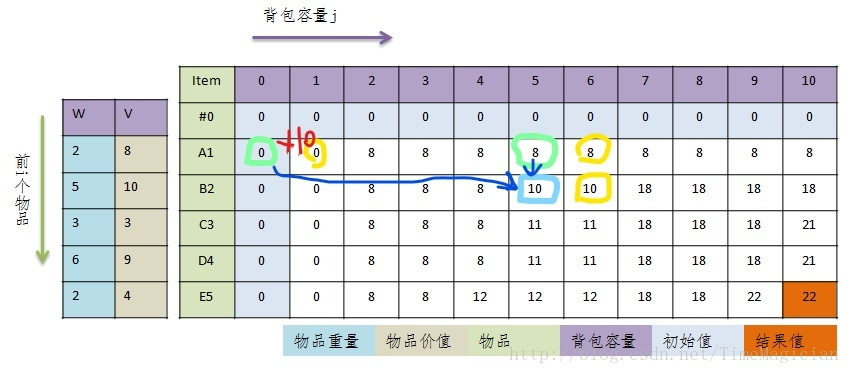
 从这张图里面还可以看出，每个宝石i的选择，其实只需要上一次的i-1时候的选择情况。因此其实可以用一个一维数组而不是二维数组表示。

d[0...W] = 0;
for i = 1->N
    for j = W->0          //这里是唯一的不同
        if(w[i] > j)
            d[j] =d[j]
        else
            d[j] = max{d[j],d[j-w[i]]+v[i]}

伪代码只是对第二个for循环的顺序做了改变。即改为了从W到0，然后就把数组换成了一维数组。

 

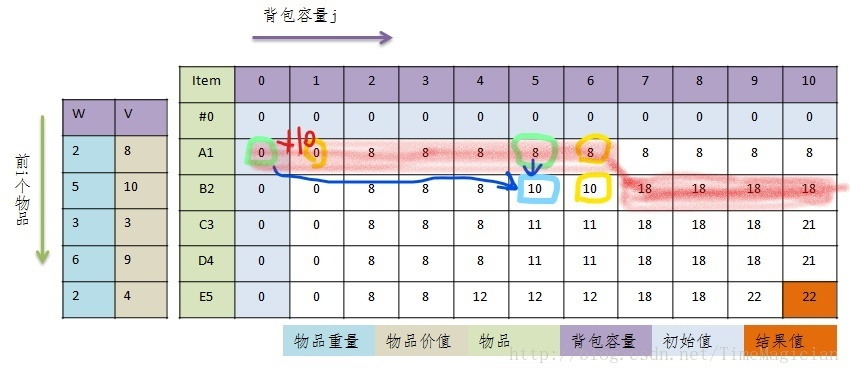
 结合上图我们可以看下发生了什么。那个一维数组内存取的东西如图红色部分（此时刻的情况是外层第一次循环后数组是 0 0 8 8 8 8 8 8 8 8 8，外层第二次循环时候内层从10 9 8 7更新）。是两个状态的结合。可以看出，当我要求d[2][6]时，我需要的d[1][6]和d[1][1],转换到一维数组时，就是d[6]和d[1]（这两个都在红色部分求出来了），然后算出来新的d[6]对原数组进行覆盖。这样就完成了空间的压缩。

 

进一步优化

在压缩到一维数组后，其实我们还可以继续优化，即对二层循环的上下限做手脚。
伪代码如下：

d[0...W] = 0;
for i = 1->N
    for j = W->w[i]          //下限不同了
    /*
    if(w[i] > j)
        d[j] =d[j]
        else
        */
     d[j] = max{d[j],d[j-w[i]]+v[i]}

为何是w[i]呢，因为当内层小于w[i]时候，说明已经是装不下了，也就不需要考虑d[j-w[i]]+v[i]这一部分，因为这一部分代表的是装下去了，再看之前的结果

 

再进一步

上一节是从左边考虑遍历的节省界限。即去掉从0开始到w[i]的部分。
这一节是从右边考虑遍历的节省界限。

 

 

---

 

下面这个回答c是占用体积，v总体积

 

 关于01背包问题九讲的优化? - hank袁榛池的回答 - 知乎 https://www.zhihu.com/question/32015129/answer/112292702

---

 

 

 

考虑对于结果第n个宝石，其考虑的就是d[W]项，那其前一项，其实只需要提供从d[W]到d[W-w[n]]项即可（这里是18和21）。如下图蓝色项。因此，对于第i个宝石时，我们指控考虑的d[j]项的范围为：W到max{w[i],W−sum(w[i],w[i+1],...,w[n])}

 

为什么可以这样做？ 给出一个理解

因为第二层循环用大于w[i]和大于W−sum(w[i],w[i+1],...,w[n]都可以解释的通，那么自然是大于较大值。

对于sum的理解是，我们把当前物品和之后所有物品都装进去了之后，剩下的空间，剩下的空间要是比w[i]大，那肯定就直接取大的那一项了（也就是W−sum(w[i],w[i+1],...,w[n]这么大空间在列表中的对应的价值）（就像上图中同一行右边大于左边）

剩下空间要是比w[i]小，那说明就要用w[i]取较大的那一项，小了就不考虑了