【XR-3】核心城市(树直径)

【XR-3】核心城市

这题真的难啊.........

k个核心城市太麻烦，我们假设先找一个核心城市，应该放在哪里?

(任意取一个点，它的最远端是直径的端点。)

(所以当这个点是直径的中点时，可以达到题目的要求(最大距离最小))

(想求中点，我们就保存直径的路径，中间的点就是中点了。)

(然后该怎么办?其余的k-1个点怎么选?)

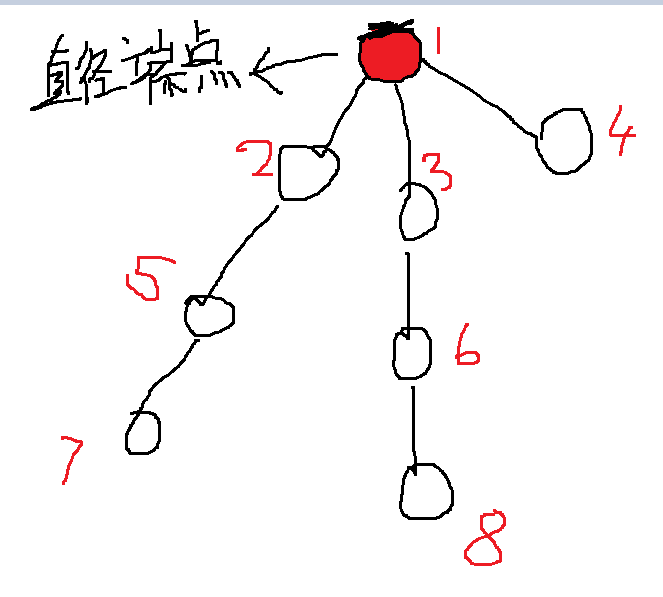
(发现7、8号节点距离可核心城市最远,目前影响答案的是他们,所以我们下一步应该把2和3号节点变成核心城市)

(至此，贪心策略已经出来了)

(在以直径中点为根的树中，我们总是选取那些maxdeep-mydeep最大的节点)

(其中maxdeep是当前节点能到的最大深度，也就是这个分支离核心城市最远的节点)

(deep是自己的深度)

#include <bits/stdc++.h>
using namespace std;
const int maxn=200009;
struct p{
	int to,nxt;
}d[maxn];int n,k,cnt=1;
int head[maxn],dis[maxn],deep[maxn],maxdeep[maxn],f[maxn];
void add(int u,int v){
	d[cnt].nxt=head[u],d[cnt].to=v,head[u]=cnt++;
}
int num,juli=0;
void dfs1(int now,int ju,int fa)
{
	if(ju>juli)
	{
		juli=ju;
		num=now;
	}
	for(int i=head[now];i;i=d[i].nxt)
	{
		int v=d[i].to;
		if(v==fa)	continue;
		dfs1(v,ju+1,now);
	}
}
void dfs2(int now,int ju,int fa)
{
	if(ju>juli)
	{
		juli=ju;
		num=now;	
	}	
	for(int i=head[now];i;i=d[i].nxt)
	{
		int v=d[i].to;
		if(v==fa)	continue;
		f[v]=now;
		dfs2(v,ju+1,now);
	}
} 
void dfsz(int now,int fa)
{
	maxdeep[now]=deep[now];
	for(int i=head[now];i;i=d[i].nxt)
	{
		int v=d[i].to;
		if(v==fa)	continue;
		deep[v]=deep[now]+1;
		dfsz(v,now);
		maxdeep[now]=max(maxdeep[now],maxdeep[v]);
	}
}
bool com(int a,int b){
	return a>b;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<n;i++)
	{
		int l,r;
		cin>>l>>r;
		add(l,r);add(r,l);
	}
	dfs1(1,0,0);//找出直径的端点 
	juli=0;
	dfs2(num,0,0);//找出直径的路径 
	int mid=num;//直径的端点 
	for(int i=1;i<=(1+juli)/2;i++)//一共经过了juli个点 
		mid=f[mid];
	dfsz(mid,0);
	for(int i=1;i<=n;i++)	deep[i]=maxdeep[i]-deep[i];
	sort(deep+1,deep+1+n,com);
	int ans=0;
	for(int i=k+1;i<=n;i++) ans=max(ans,deep[i]+1);
	cout<<ans;
}