《算法竞赛进阶指南》 第一章 Acwing 99. 激光炸弹 二维前缀和

地址 https://www.acwing.com/problem/content/description/101/

地图上有 N 个目标，用整数 Xi,Yi 表示目标在地图上的位置，每个目标都有一个价值 Wi。

注意：不同目标可能在同一位置。

现在有一种新型的激光炸弹，可以摧毁一个包含 R×R 个位置的正方形内的所有目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和 x，y 轴平行。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式
第一行输入正整数 N 和 R，分别代表地图上的目标数目和正方形的边长，数据用空格隔开。

接下来 N 行，每行输入一组数据，每组数据包括三个整数 Xi,Yi,Wi，分别代表目标的 x 坐标，y 坐标和价值，数据用空格隔开。

输出格式
输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围
0≤R≤109
0<N≤10000,
0≤Xi,Yi≤5000
0≤Wi≤1000
输入样例：
2 1
0 0 1
1 1 1
输出样例：
1

解法

计算每个边长为r的正方形能覆盖的价值

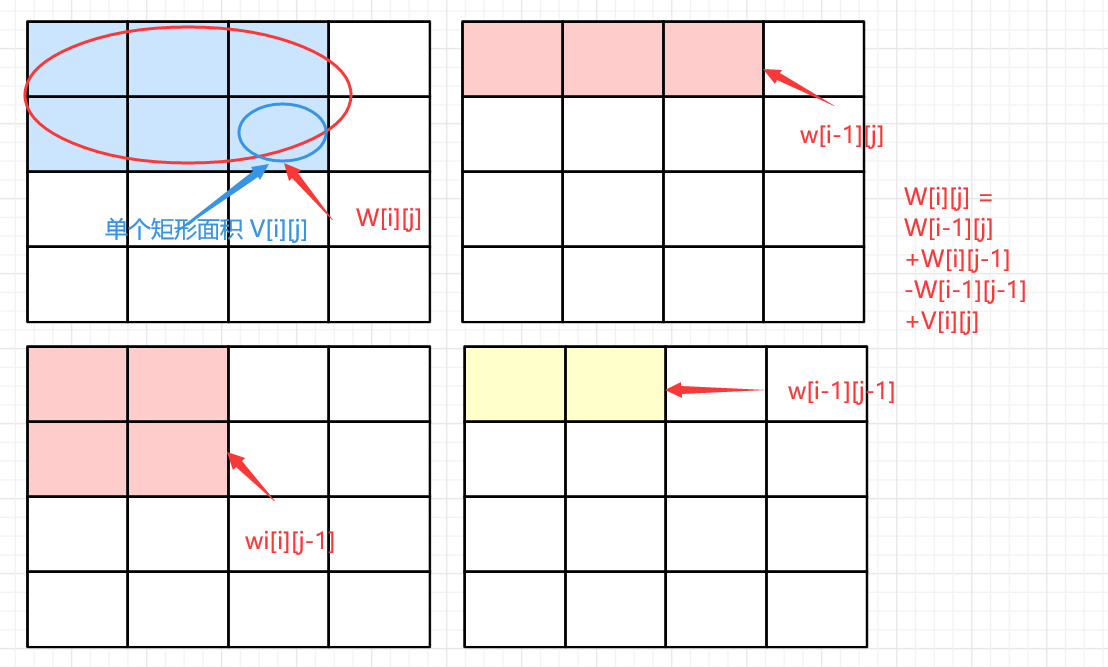
使用二维前缀和进行区间计算的加速  V代表单个矩形的面积  W[i][j]代表从0,0坐标开始到i,j坐标的多个矩形的面积和

W[i][j] = W[i-1][j]+W[i][j-1] - W[i-1][j-1] + V[i][j]

减去W[i-1][j-1] 是因为 W[i-1][j]+W[i][j-1]中将前者加了两次 所以要减少一次

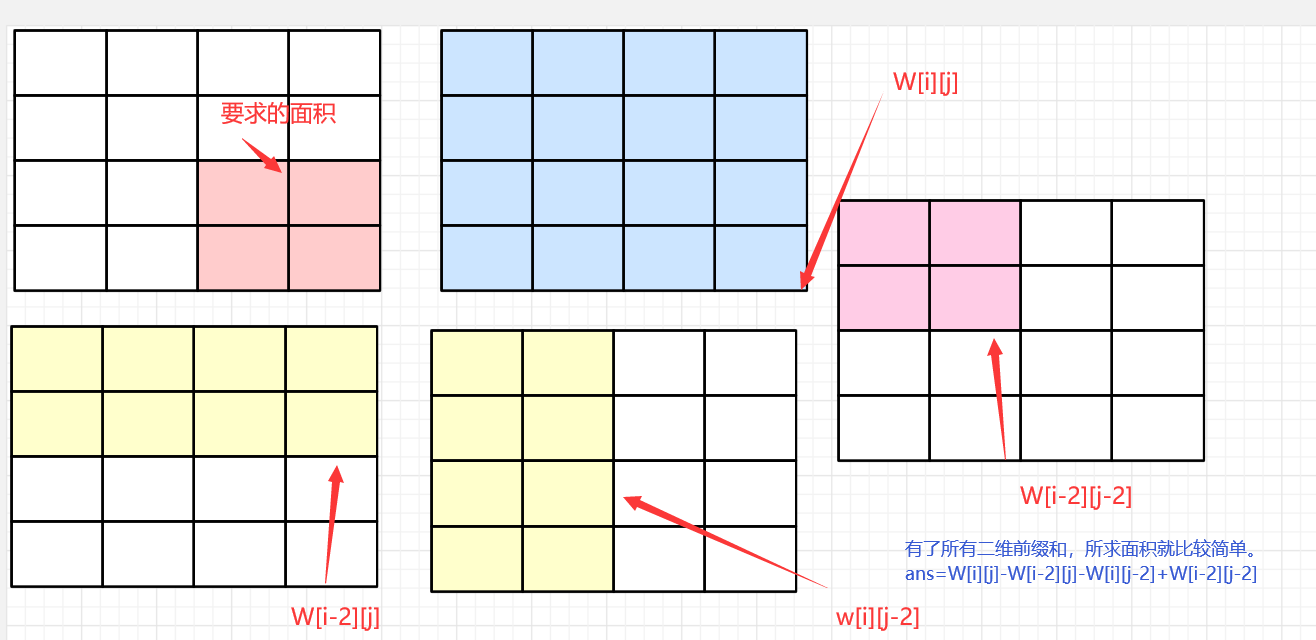
当我们计算完所有W[i][j]  那么利用前缀和公式可以快速的获取任意 左上坐标为jk到右下坐标的矩形面积和

 需要注意的点

1 为了计算前缀和方便 整个地图 xy均加上了1   因为前缀和有类似 a[i] = a[i]+a[i-1]的操作，i等于0要处理边界。 二维前缀和也类似

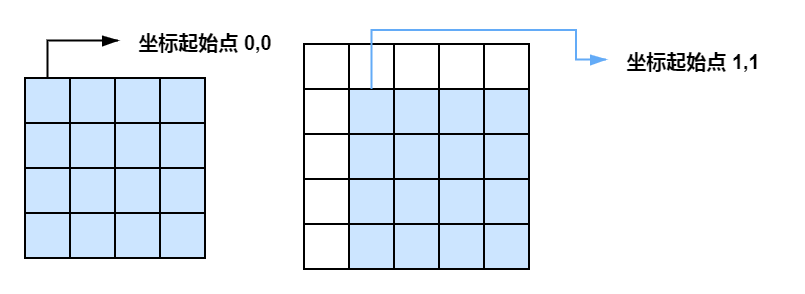
2 矩形能覆盖的图形只包括举证的下边和右边 不包括上边和左边。我怀疑是题目为了吻合前缀和的解法，强行解释数据的问题。

一个炸弹轰炸面积是正方形且还要边平行于XY轴 左上点是归属于W[i][j]  右下角点是归属于W[i+1][j+1]

一个边长是两者之差的炸弹矩形面积是无法同时包括两点 这就很诡异了 除了用前缀和解释。

3 给出的炸弹覆盖矩形范围的边长 大于整个地图，注意处理

#include <iostream>
#include <algorithm>


using namespace std;


const int N = 5010;
int val[N][N];

int r, cnt;

int main()
{
    cin >> cnt >> r;
    r = min(5000,r);

    for (int i = 0; i < cnt; i++) {
        int x, y, v;
        cin >> x >> y >> v;
        val[x+1][y+1] += v;
    }

    //计算二维前缀和
    for (int i = 1; i <= 5001; i++) {
        for (int j = 1; j <= 5001; j++) {
            val[i][j] += val[i - 1][j] + val[i][j - 1] - val[i - 1][j - 1];
        }
    }
    int ans = 0;
    //以右下角为起点 找到整个变长为r的正方形覆盖的价值
    for (int i = r; i <= 5001; i++) {
        for (int j = r; j <= 5001; j++) {
            ans = max(ans, val[i][j] - val[i - r][j] - val[i][j - r] + val[i - r][j - r]);
        }
    }

    cout << ans << endl;

}