地址 https://leetcode-cn.com/problems/minimum-path-sum/
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
解答 动态规划题目
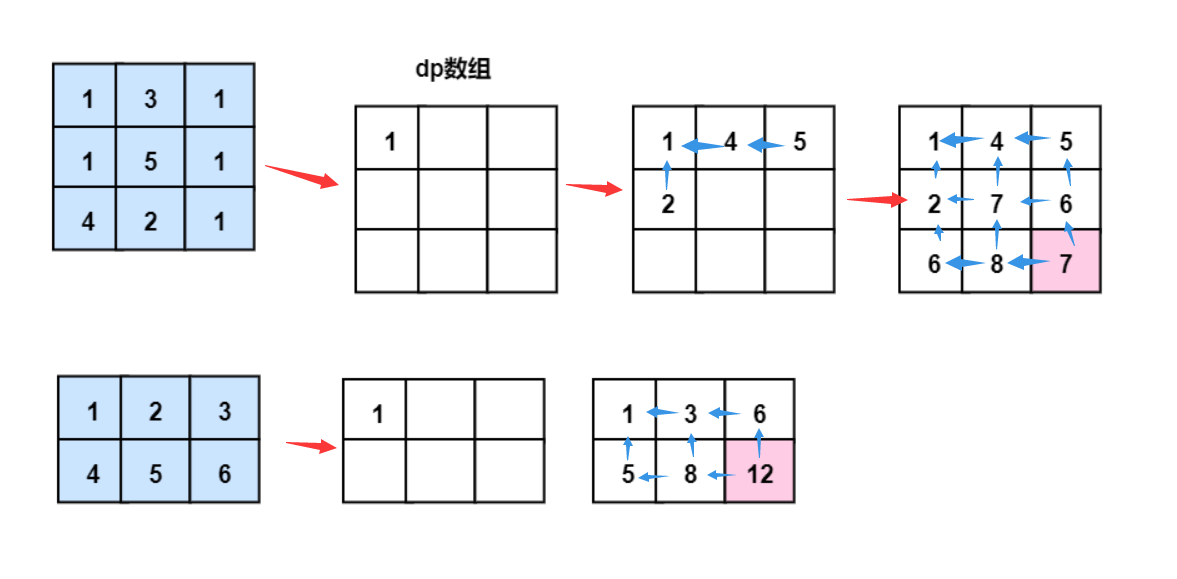
如图
动态数组表示每个格子能获取的最小值。
由于每次只能向下和向右移动。
那么每个格子的最小取值只能在该格子的左端的格子和上端的格子的最小值中取其一。
转移方程就是
dp[i][j] = min(dp[i-1][[j]+grid[i][j] , dp[i][j-1]+grid[i][j]);
那么代码如下
class Solution {
public:
int dp[300][300];
int minPathSum(vector<vector<int>>& grid) {
memset(dp,0x3f,sizeof dp);
dp[0][0] = grid[0][0];
for(int i = 0; i < grid.size();i++){
for(int j = 0; j < grid[0].size();j++){
if(j-1 >=0)
dp[i][j] = min(dp[i][j],dp[i][j-1]+grid[i][j]);
if(i-1>=0)
dp[i][j] = min(dp[i][j],dp[i-1][j]+grid[i][j]);
}
}
return dp[grid.size()-1][grid[0].size()-1];
}
};

