登陆

还是个水题QwQ
还是先来一句话题意：给定n个区间[l,r]，每个区间在这整段时间内都要独自占用一份资源，求最少几份资源能够满足所有区间

还是先看数据，第一部分，我还是不知道怎么做，就当是给各路鬼畜做法准备的吧

解法一：差分+离散化

没有学过差分的同学请百度一篇博客学一学吧，差分还是个简单的东西的，当然不想学的可以直接跳解法二

可以想到，差分的套路，每次区间开头，在差分数组++，在区间结尾恰好后一位置，差分数组--。

那么我们按照序列坐标跑一遍差分数组，即s[i]+=s[i-1]，再从中取出差分数组的最大值即可

大致模拟一下这个过程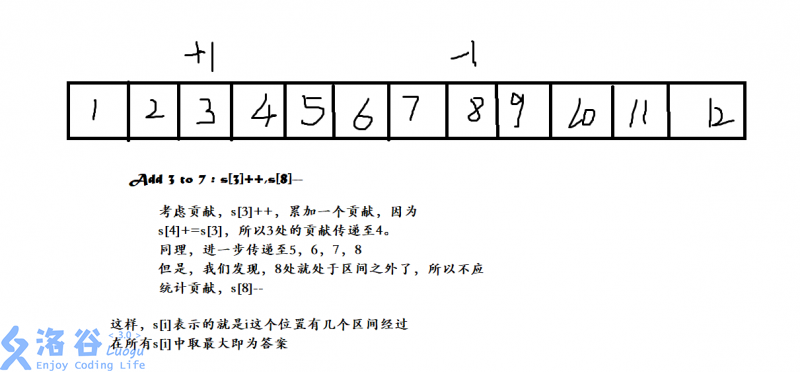



所以最终复杂度就是线性的区间个数加上坐标范围

但是只能得70%分，因为100%的数据坐标很大啊

再加上离散化就可以AC了,这里就不再赘述离散化的具体实现了，大家可以自行百度

#include<iostream>
#include<cstdio>
#include<algorithm>
#define int long long
using namespace std;
struct node{
    int l,r;
}a[100010];
int n,ans,cnt,mp[200010],tot,s[200010];
signed main()
{
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld%lld",&a[i].l,&a[i].r);
        mp[++cnt]=a[i].l,mp[++cnt]=a[i].r;
    }
    sort(mp+1,mp+cnt+1);
    cnt=unique(mp+1,mp+cnt+1)-mp-1;
    for(int i=1;i<=n;i++)
    {
        a[i].l=lower_bound(mp+1,mp+cnt+1,a[i].l)-mp;
        a[i].r=lower_bound(mp+1,mp+cnt+1,a[i].r)-mp;
        s[a[i].l]++,s[a[i].r+1]--;
    }
    for(int i=1;i<=cnt;i++)
    {
        s[i]+=s[i-1];
        ans=max(ans,s[i]);
    }
    printf("%lld
",ans);
    return 0;
}

解法二：贪心

按照开始进攻的时间把进攻排序

维护一个数组S，记录当前每个编队安排进去的最后一次打击，最初没有编队

依次对于每次进攻，扫描数组S，找到任意一个编队，满足当前的进攻开始时间不早于编队的最后一次打击的结束时间。如果这样的编队不存在，则新建一个编队。

这个贪心算法的时间复杂度是O(n^2)，请读者自行证明其正确性。这样就得到了30%

我们可以用一个小根堆维护每个编队最后一次打击结束的时间，尝试把当前的进攻安排在堆顶（结束时间最早）的编队下。这样时间复杂度就可以降低到O(nlogn)

#include<iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
#define int long long
using namespace std;
struct node{
    int l,r,id;
}a[1000010];
struct data{
    int id,t;
};
priority_queue<data>q;
int n,ans[1000010],cnt;
bool cmp(const node &x,const node &y)
{
    return x.l<y.l;
}
bool operator <(const data &x,const data &y)
{
    return x.t>y.t;
}
signed main()
{
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)
        scanf("%lld%lld",&a[i].l,&a[i].r),a[i].id=i;
    sort(a+1,a+n+1,cmp);
    q.push((data){++cnt,a[1].r}),ans[a[1].id]=cnt;
    for(int i=2;i<=n;i++)
    {
        data u=q.top();
        q.pop();
        if(a[i].l>u.t)
            q.push((data){u.id,a[i].r}),ans[a[i].id]=u.id;
        else
            q.push((data){++cnt,a[i].r}),q.push(u),ans[a[i].id]=cnt;
    }
    printf("%lld
",cnt);
    return 0;
}

解法三：还是贪心，只是用set维护

来自@_23333神犇的想法

按最早进攻时间对进攻排序

对于每次进攻

把进攻结束时间之后（即可以下次打击的最早时间）扔进$set$

每次从set中lower_bound

如果这之前没有能够继续的编队，就新建一个

否则用那个继续这次进攻

#include<bits/stdc++.h>
#define N 100005
#define l first
#define r second
#define pr pair<int,int>
#define int long long
using namespace std;

inline void rd(int &X)
{
    X=0;int w=0;char ch=0;
    while(!isdigit(ch))w|=ch=='-',ch=getchar();
    while( isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    X=w?-X:X;
}

int n;
multiset<int> s;
multiset<int> :: iterator it;
pr a[N];

signed main()
{
    rd(n);
    for(int i=1;i<=n;i++)
        rd(a[i].l),rd(a[i].r);
    sort(a+1,a+1+n);
    s.insert(a[1].r+1);
    for(int i=2;i<=n;i++)
    {
        it=s.upper_bound(a[i].l);
        if(it==s.begin())
            s.insert(a[i].r+1);
        else {
            it--;
            s.erase(it);
            s.insert(a[i].r+1);
        }
    }
    cout<<s.size();
}