Chessboard
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 11078 | Accepted: 3449 |
Description
Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below). 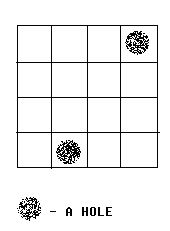
Some examples are given in the figures below: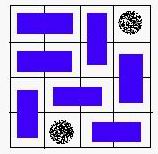 A VALID solution.
A VALID solution.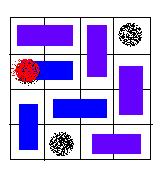 An invalid solution, because the hole of red color is covered with a card.
An invalid solution, because the hole of red color is covered with a card.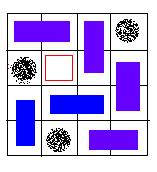 An invalid solution, because there exists a grid, which is not covered.
An invalid solution, because there exists a grid, which is not covered.

Some examples are given in the figures below:
 A VALID solution.
A VALID solution. An invalid solution, because the hole of red color is covered with a card.
An invalid solution, because the hole of red color is covered with a card. An invalid solution, because there exists a grid, which is not covered.
An invalid solution, because there exists a grid, which is not covered.Input
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.
Output
If the board can be covered, output "YES". Otherwise, output "NO".
Sample Input
4 3 2 2 1 3 3
Sample Output
YES
Hint
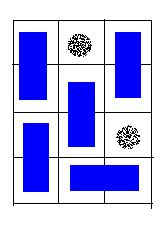 A possible solution for the sample input.
A possible solution for the sample input.Source
POJ Monthly,charlescpp
独立集:
独立集是指图的顶点集的一个子集,该子集的导出子图不含边.如果一个独立集不是任何一个独立集的子集, 那么称这个独立集是一个极大独立集.一个图中包含顶点数目最多的独立集称为最大独立集。最大独立集 一定是极大独立集,但是极大独立集不一定是最大的独立集。
支配集:
与独立集相对应的就是支配集,支配集也是图顶点集的一个子集,设S 是图G 的一个支配集,则对于图中的任意一个顶点u,要么属于集合s, 要么与s 中的顶点相邻。 在s中除去任何元素后s不再是支配集,则支配集s是极小支配集。称G的所有支配集中顶点个数最 少的支配集为最小支配集,最小支配集中的顶点个数成为支配数。
最小点的覆盖:
最小点的覆盖也是图的顶点集的一个子集,如果我们选中一个点,则称这个点将以他为端点的所有边都覆盖了。将图中所有的边都覆盖所用顶点数最少,这个集合就是最小的点的覆盖。
最大团:
图G的顶点的子集,设D是最大团,则D中任意两点相邻。若u,v是最大团,则u,v有边相连,其补图u,v没有边相连,所以图G的最大团=其补图的最大独立集。
一些性质:
最大独立集+最小覆盖集=V
最大团=补图的最大独立集
最小覆盖集=最大匹配
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int m,n,k,tot; int map[1610][1610],g[40][40],tg[40][40]; int linker[1610],vis[1610]; int DFS(int u){ int v; for(v=1;v<=tot;v++) if(map[u][v] && !vis[v]){ vis[v]=1; if(linker[v]==-1 || DFS(linker[v])){ linker[v]=u; return 1; } } return 0; } int Hungary(){ int u,ans=0; memset(linker,-1,sizeof(linker)); for(u=1;u<=tot;u++){ memset(vis,0,sizeof(vis)); if(DFS(u)) ans++; } return ans; } int main(){ //freopen("input.txt","r",stdin); while(~scanf("%d%d%d",&m,&n,&k)){ int x,y; memset(g,0,sizeof(g)); while(k--){ scanf("%d%d",&x,&y); g[y][x]=1; //注意这里是y行x列,被WA了好几次。。。。。。。。。。。。 } tot=0; memset(tg,0,sizeof(tg)); for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) if(g[i][j]==0) tg[i][j]=++tot; memset(map,0,sizeof(map)); for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) if(tg[i][j]!=0){ if(i>=1 && tg[i-1][j]!=0) map[tg[i][j]][tg[i-1][j]]=1; if(i<=m && tg[i+1][j]!=0) map[tg[i][j]][tg[i+1][j]]=1; if(j>=1 && tg[i][j-1]!=0) map[tg[i][j]][tg[i][j-1]]=1; if(j<=n && tg[i][j+1]!=0) map[tg[i][j]][tg[i][j+1]]=1; } int ans=Hungary(); if(ans==tot) puts("YES"); else puts("NO"); } return 0; }