|
Similarity of necklaces 2
Description The background knowledge of this problem comes from "Similarity of necklaces". Do not worry. I will bring you all the information you need.
The little cat thinks about the problem he met again, and turns that problem into a fair new one, by putting N * (N + 1) / 2 elements into a linear list, with M = N * (N + 1) / 2 elements:  (The above table denotes Table and Pairs in description of after converting) One more array named "Multi" appears here. Suppose Pairs and Multi are given, the little cat's purpose is to determine an array Table with M integers that obey:  (this condition is similar with the condition 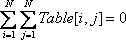 that appears in the problem "Similarity of necklaces") and make 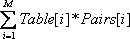 as large as possible. What is more, we must have Low[i] <= Table[i] <= Up[i] for any 1 <= i <= M. Here Low and Up are two more arrays with M integers given to you. Input The input contains a number of test cases. Each of the following blocks denotes a single test case. A test case starts by an integer M (1 <= M <= 200) and M lines followed. The i-th line followed contains four integers: Pairs[i], Multi[i], Low[i], Up[i].
Restrictions: -25 <= Low[i] < Up[i] <= 25, 0 <= Pairs[i] <= 100000, 1 <= Multi[i] <= 20. From the input given, you may assume that there is always a solution. Output For each test case, output a single line with a single number, which is the largest
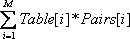 Sample Input 10 7 1 1 10 0 2 -10 10 2 2 -10 10 0 2 -10 10 0 1 1 10 0 2 -10 10 0 2 -10 10 0 1 1 10 0 2 -10 10 0 1 1 10 10 0 1 1 10 2 2 -10 10 2 2 -10 10 2 2 -10 10 0 1 1 10 2 2 -10 10 2 2 -10 10 0 1 1 10 2 2 -10 10 0 1 1 10 Sample Output 90 -4 Source POJ Monthly--2006.01.22,Zeyuan Zhu
|
Similarity of necklaces 2
这个问题是一个012背包问题。我们知道01背包只要逆向线性检索,无限背包只要正向检索。012背包就是说,每个物品有一个数量上限。这个问题可以用log方法,也存在线性方法,需要维护一个递增/递减序列。
我们先把所有的Table都放成下限,接下来我们可以算出它距离总和为0还需要增加多少。对于1<=i<=M,它可以看成这样一个物品:体积为Multi[i],费用为Pairs[i],数量为Up[i]-Low[i]。然后就得到一个012背包问题了。
复杂度约为:O(M*背包大小)。其中背包大小不超过M*20*25=200*20*25=100000。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 6 using namespace std; 7 8 const int INF=0x3f3f3f3f; 9 const int maxn=220; 10 11 int P[maxn],M[maxn],cnt[maxn]; 12 int dp[100010]; 13 int n,V,val; 14 15 void ZeroOnePack(int cost,int weight){ 16 for(int i=V;i>=cost;i--) 17 dp[i]=max(dp[i],dp[i-cost]+weight); 18 } 19 20 void CompletePack(int cost,int weight){ 21 for(int i=cost;i<=V;i++) 22 dp[i]=max(dp[i],dp[i-cost]+weight); 23 } 24 25 void MultiplePack(int cost,int weight,int amount){ 26 if(cost*amount>=V){ 27 CompletePack(cost,weight); 28 return ; 29 } 30 int k=1; 31 while(k<=amount){ 32 ZeroOnePack(k*cost,k*weight); 33 amount-=k; 34 k<<=1; 35 } 36 ZeroOnePack(amount*cost,amount*weight); 37 } 38 39 int main(){ 40 41 //freopen("input.txt","r",stdin); 42 43 while(~scanf("%d",&n)){ 44 V=0,val=0; 45 int low,up; 46 for(int i=1;i<=n;i++){ 47 scanf("%d%d%d%d",&P[i],&M[i],&low,&up); 48 V+=low*M[i]; 49 val+=low*P[i]; 50 cnt[i]=up-low; 51 } 52 V=-V; 53 memset( dp, 128, sizeof(dp)); //127,128,129都可以,但是why??? 54 dp[0] = 0; 55 //memset(dp,0,sizeof(dp)); 56 for(int i=1;i<=n;i++) 57 MultiplePack(M[i],P[i],cnt[i]); 58 printf("%d\n",dp[V]+val); 59 } 60 return 0; 61 }