模拟退火算法及其Matlab实现

1基本原理：

         模拟退火算法源于固体的退火过程，当把一个固体的加热使其升温，其内部分子出现无序状态，内能增大

而降温时，所有粒子趋于有序，冷却到最低温度时内能达到最少。当某一状态下系统内能减少，则完全

接受这一新的状态，否则对于这一状态采样概率接受，温度越高，接受的概率越大。当温度由初始值逐渐

降到最低温度时，即可得到最低的内能，也就是算法的最优解。

2算法步骤：

  （1）设置算法的参数：初始温度，结束温度，温度衰减系数，每个温度下的扰动次数，初始状态，初始解

   （2）对状态产生扰动，计算新状态下的解，比较两个解的大小，判断是否接受新的状态

   （3）在此温度下，对步骤（2）按设置的扰动次数重复进行扰动

   （4）对温度进行衰减，并在新的温度下重复（2）（3），直到结束温度

   （5）输出记录最优状态和最优解，算法结束

3实例计算：

  采用TSP问题中的eil51数据，官方的最优解为426，编写Matlab程序，进行计算

4Matlab代码：

clc,clear            %清空环境中的变量
tic
iter = 1;                                                                                   % 迭代次数初值
a=0.99;                                                                                    %温度衰减系数
t0=120;                                                                                    %初始温度
tf=1;                                                                                          %最后温度
t=t0;
Markov=10000;                                                                     %Markov链长度
load data1.txt                                                                           %读入城市的坐标
city=data1;
n = size(city,1);                                                                      %城市距离初始化
D = zeros(n,n);                                                    
for i = 1:n
    for j = 1:n
            D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^2));
    end    
end                                                                                
route=1:n;   
route_new=route;
best_length=Inf;
Length=Inf;
best_route=route;
%%
while t>=tf
            for j=1:Markov
                    %进行扰动,长生新的序列route_new;
                    if (rand<0.7)
                        %交换两个数的顺序
                           ind1=0;ind2=0;
                           while(ind1==ind2&&ind1>=ind2)
                                    ind1=ceil(rand*n);
                                    ind2=ceil(rand*n);
                           end                      
                                      temp=route_new(ind1);
                                      route_new(ind1)=route_new(ind2);
                                      route_new(ind2)=temp;
                    else
                          ind=zeros(3,1);
                          L_ind=length(unique(ind));
                          while (L_ind<3)
                                    ind=ceil([rand*n rand*n rand*n]);
                                    L_ind=length(unique(ind));
                          end
                          ind0=sort(ind);
                          a1=ind0(1);b1=ind0(2);c1=ind0(3);
                         route0=route_new;
                         route0(a1:a1+c1-b1-1)=route_new(b1+1:c1);
                         route0(a1+c1-b1:c1)=route_new(a1:b1);
                         route_new=route0;    
                    end 
                     %计算路径的距离,Length_new 
                          length_new = 0;
                        Route=[route_new route_new(1)];
                              for j = 1:n
                                  length_new = length_new+ D(Route(j),Route(j + 1));
                              end
                     if length_new<Length      
                              Length=length_new;
                              route=route_new;
                           %对最优路线和距离更新
                           if       length_new<best_length
                                    iter = iter + 1;    
                                     best_length=length_new;
                                     best_route=route_new;
                           end
                     else
                             if rand<exp(-(length_new-Length)/t)
                                  route=route_new;
                                  Length=length_new;
                              end
                     end
                       route_new=route; 
                end              
                        t=t*a;
end

%--------------------------------------------------------------------------
%% 结果显示 
toc
Route=[best_route best_route(1)];
plot([city(Route ,1)], [city(Route ,2)],'o-');
    disp('最优解为：')
    disp(best_route)
    disp('最短距离：')
    disp(best_length)
    disp('最优解迭代次数：')
    disp(iter)
for i = 1:n
    %对每个城市进行标号
    text(city(i,1),city(i,2),['   ' num2str(i)]);
end
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['模拟退火算法(最短距离）:' num2str(best_length) ''])

5运行结果：

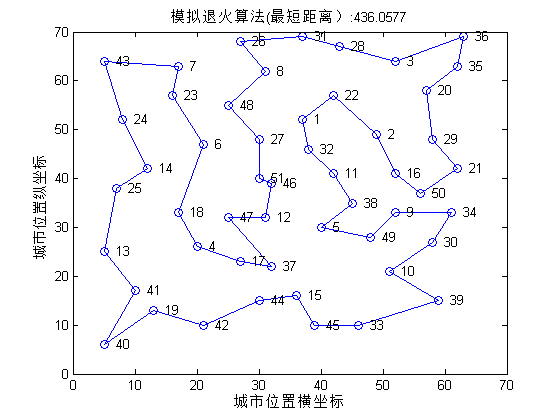
最短距离：436.7146，其和最优解426接近

TSP图：