3、数组
对于很多语言,都会有数组(array)这种基本的数据结构
还是先来看看定义
数组是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
数据里面的每个变量叫做元素
里面有几个关键点,分别是线性表和连续的内存空间
先来看看线性表
什么叫线性表呢?顾名思义,线性表就是数据排成像一条线一样的结构。在通俗一点就是
把所有数据用一根线儿串起来
除了数组以外,链表、队列、栈等也是线性表结构。


当然与之对应的叫做非线性表,比如二叉树、堆、图等。之所以叫非线性,是因为,在非线性表中,所有数据不能用一根线从头到尾串起来
比如下面的树(上)和图(下)的结构
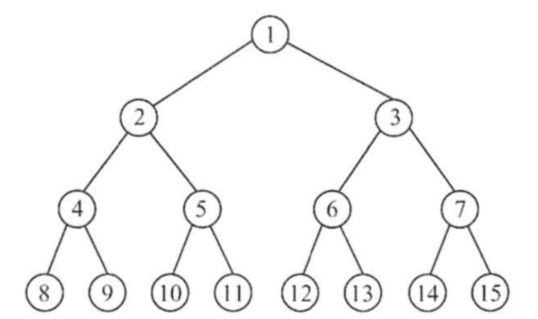
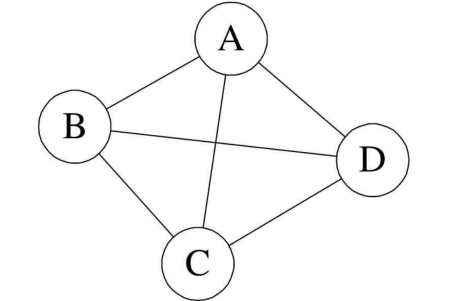
再来说说连续的内存空间
正在因为这个特点:数组有了“随机访问”的特性。但有利就有弊,这也让插入。删除操作变得非常低效,为了保证连续性,就需要做大量的数据搬移工作。
数据的基本操作
随机访问和更新元素
比如我们这里申明了这样一个整数数组
int[] a = new int[10]
里面可以装10个元素 我们可以通过a[0]来访问第一个元素,a[n]来访问n+1个元素
([]中的数字叫做下标,从0开始
数组的长度我们可以通过数组的length属性来获得 比如上面的a数组 就是a.length)
根据数组的下标 我们知道 随机访问一个元素的时间复杂度是O(1)
更新元素也是比较简单的
获取了以后 直接赋值即可
比如 我们这里申明并赋值了一个数组
int[] a = {1,2,3,4,5};
我们想更新下标为2的元素的值为22
a[2] = 22;
插入
假设数组的长度为 n,现在,如果我们需要将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾出来,给新来的数据,我们需要将第 k~n 这部分的元素都顺序地往后挪一位。

当然 如果直接在5号位置(相当于在末尾)上插入数据,则不用移动数据,直接插入即可
特殊的情况
但是这里有一种很特殊的情况,就是如果本身数组的大小为10,已经满了,在插入新的元素,要怎么办?
这里就涉及数组的扩容了,但是我们知道,数组的长度在创建的时候就已经确定了,那怎么处理
一个简单的思路就是创建新的更大的数组(比如直接翻倍),把原来的数据拷贝过去,然后再插入
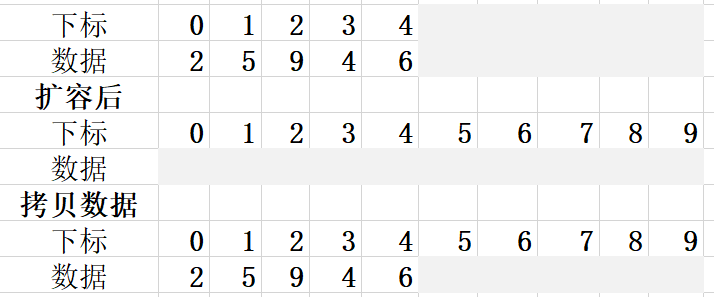
删除
数组删除元素时候,只要数组的元素不在末尾,其后的元素都要往前挪动一位

其实删除的时候还有另外一种操作,比如我们要删除2号位置上的元素,我们直接让最后一位有数据的元素和2号元素交换,然后在删除最后一位有数据的元素,这样子就避免了数据的移动,当然这种方式仅仅作为参考,并不是删除元素的主流操作。
其他
1、数组越界
数组越界在 C 语言中是一种未决行为,也就是不会报错。编译器并没有处理数组越界的情况。因为,访问数组的本质就是访问一段连续内存,只要数组通过偏移计算得到的内存地址是可用的,那么程序就可能不会报任何错误。
但是Java 本身就会做越界检查,比如下面这几行 Java 代码,就会抛出 java.lang.ArrayIndexOutOfBoundsException异常
int[] a = new int[3];
a[5] = 1;
2、为啥大部分编程语言的下标从0开始?大家可以了解了解
先不说原因哈,像这类问题,一般可以盲猜一波
计算机类的原因 无外乎就性能原因 历史原因,或者就是个人喜好等
我查阅了一些资料
关于性能原因的解释
从数组存储的内存模型上来看,“下标”最确切的定义应该是偏移(offset)。
如果用 a 来表示数组的首地址,a[0]就是偏移为 0 的位置,也就是首地址,
a[k]就表示偏移 k 个 type_size 的位置,
所以计算 a[k]的内存地址只需要用这个公式
a[k]_address = base_address + k * type_size
但是,如果数组从 1 开始计数,
那我们计算数组元素 a[k]的内存地址就会变为:
a[k]_address = base_address + (k-1)*type_size
对比两个公式,我们不难发现,从 1 开始编号,每次随机访问数组元素都多了一次减法运算,对于 CPU 来说,就是多了一次减法指令。
数组作为非常基础的数据结构,通过下标随机访问数组元素又是其非常基础的编程操作,
效率的优化就要尽可能做到极致。
所以为了减少一次减法操作,数组选择了从 0 开始编号,而不是从 1 开始。
但是也有可能是历史原因
C 语言设计者用 0 开始计数数组下标,之后的 Java、JavaScript 等高级语言都效仿了 C 语言,
或者说,为了在一定程度上减少 C 语言程序员学习 Java 的学习成本(就像现在很多语言其实都有一定的相似度,能够减少我们的学习成本)
因此继续沿用了从 0 开始计数的习惯。实际上,很多语言中数组也并不是从 0 开始计数的,比如 Matlab。甚至还有一些语言支持负数下标,比如 Python。