高斯消元:最直接的用法是解N元一次方程组
可以将每一个位置数的系数以及每个方程的答案列成矩阵
考虑小学解二元一次方程组的两种办法,一种是代入消元法,一种是加减消元法
代入消元法不确定性高,相比之下,加减消元法更适合代码实现,模拟加减消元法
的过程,实际上就是在做高斯消元
实现:
依次处理每个未知数,假设在处理第i个未知数,找到第i个未知数中最大的一个,
(假如最大值为0,即全部系数都是0,则这个方程无解)放到(i,i),然后通过这个方程全部除Ai使第i项
系数化为1,再枚举每个方程,令r = f[j][i],每一项都减去(f[i][k]*r),一个系数就消去了
如此重复,最终只剩下上三角矩阵,如图:
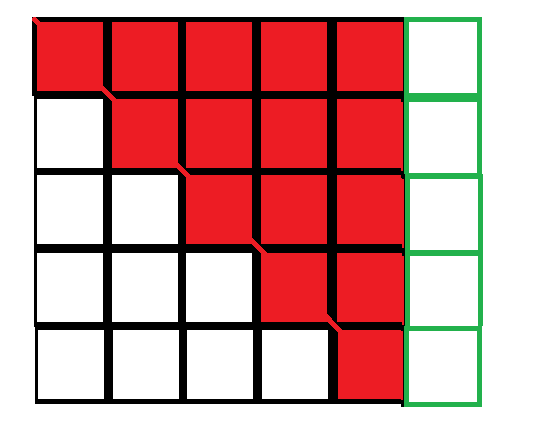
这时候从第n个方程开始,逐个得出解,再进行回带,就可以解出所有未知数
code
#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; double map[111][111]; double ans[111]; double eps=1e-7; int main(){ int n; cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n+1;j++) scanf("%lf",&map[i][j]); for(int i=1;i<=n;i++){ int r=i; for(int j=i+1;j<=n;j++) if(fabs(map[r][i])<fabs(map[j][i])) r=j;//find_the_biggest_number_of_the_first_column(at present) if(fabs(map[r][i])<eps){ printf("No Solution"); return 0; } if(i!=r)swap(map[i],map[r]);//对换一行或一列,属于找最大当前系数的其中一步。(这样就可以只处理当前行的系数啦!) double div=map[i][i]; for(int j=i;j<=n+1;j++) map[i][j]/=div; for(int j=i+1;j<=n;j++){ div=map[j][i]; for(int k=i;k<=n+1;k++) map[j][k]-=map[i][k]*div; } } ans[n]=map[n][n+1]; for(int i=n-1;i>=1;i--){ ans[i]=map[i][n+1]; for(int j=i+1;j<=n;j++) ans[i]-=(map[i][j]*ans[j]); }//回带操作 for(int i=1;i<=n;i++) printf("%.2lf ",ans[i]); }
code by Flower_pks